# Expresiones aritméticas - Gráficas Bonitas


[Verano 2016 - Ive - Rafa]
Las expresiones aritméticas son parte esencial de casi cualquier algoritmo que resuelve un problema útil. Por lo tanto, implementar expresiones aritméticas correctamente es una destreza básica en cualquier lenguaje de programación de computadoras. En esta experiencia de laboratorio practicarás la implementación de expresiones aritméticas en C++ escribiendo ecuaciones paramétricas para graficar curvas interesantes.
## Objetivos:
1. Implementar expresiones aritméticas en C++ para producir gráficas.
2. Utilizar constantes adecuadamente.
3. Definir variables utilizando tipos de datos adecuados.
4. Convertir el valor de un dato a otro tipo cuando sea necesario.
## Pre-Lab:
Antes de llegar al laboratorio debes haber:
1. Repasado los siguientes conceptos:
a. implementar expresiones aritméticas en C++
b. tipos de datos nativos de C++ (int, float, double, char)
c. usar "type casting" para covertir el valor de una variable a otro tipo dentro de expresiones.
d. utilizar funciones y constantes aritméticas de la biblioteca `cmath`
e. la ecuación y gráfica de un círculo
2. Estudiado los conceptos e instrucciones para la sesión de laboratorio.
3. Tomado el quiz Pre-Lab que se encuentra en Moodle.
---
---
## Ecuaciones paramétricas
Las *ecuaciones paramétricas* nos permiten representar una cantidad como función de una o más variables independientes llamadas *parámetros*. En muchas ocasiones resulta útil representar curvas utilizando un conjunto de ecuaciones paramétricas que expresen las coordenadas de los puntos de la curva como funciones de los parámetros. Por ejemplo, en tu curso de trigonometría debes haber estudiado que la ecuación de un círculo con radio $$r$$ y centro en el origen tiene una forma así:
$$x^2+y^2=r^2.$$
Los puntos $$(x,y)$$ que satisfacen esta ecuación son los puntos que forman el círculo de radio $$r$$ y centro en el origen. Por ejemplo, el círculo con $$r=2$$ y centro en el origen tiene ecuación
$$x^2+y^2=4,$$
y sus puntos son los pares ordenados $$(x,y)$$ que satisfacen esa ecuación. Una forma paramétrica de expresar las coordenadas de los puntos de el círculo con radio $$r$$ y centro en el origen es:
$$x=r \cos(t)$$
$$y=r \sin(t),$$
donde $$t$$ es un parámetro que corresponde a la medida (en radianes) del ángulo positivo con lado inicial que coincide con la parte positiva del eje de $$x$$, y lado terminal que contiene el punto $$(x,y)$$, como se muestra en la Figura 1.
---
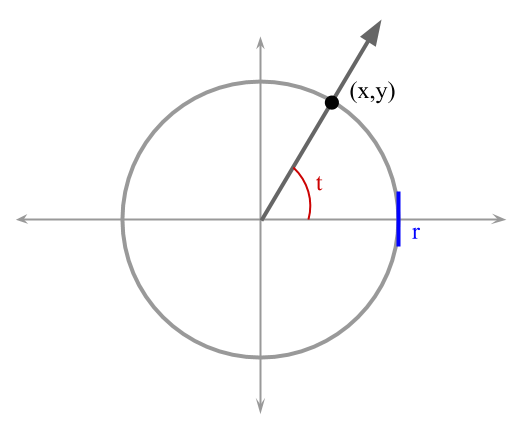
**Figura 1.** Círculo con centro en el origen y radio $$r$$.
---
Para graficar una curva que está definida usando ecuaciones paramétricas, computamos los valores de $$x$$ y $$y$$ para un conjunto de valores del parámetro. Por ejemplo, la Figura 2 resalta algunos valores de $$t$$, $$(x,y)$$ para el círculo con $$r = 2$$.
---
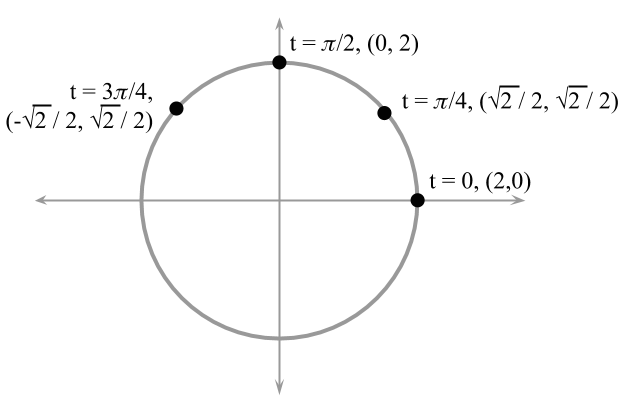
**Figura 2.** Algunas coordenadas de los puntos $$(x,y)$$ del círculo con radio $$r=2$$ y centro en el origen.
---
---
!INCLUDE "../../eip-diagnostic/pretty-plots/es/diag-pretty-plots-01.html"
!INCLUDE "../../eip-diagnostic/pretty-plots/es/diag-pretty-plots-02.html"
!INCLUDE "../../eip-diagnostic/pretty-plots/es/diag-pretty-plots-03.html"
!INCLUDE "../../eip-diagnostic/pretty-plots/es/diag-pretty-plots-04.html"
!INCLUDE "../../eip-diagnostic/pretty-plots/es/diag-pretty-plots-05.html"
!INCLUDE "../../eip-diagnostic/pretty-plots/es/diag-pretty-plots-06.html"
!INCLUDE "../../eip-diagnostic/pretty-plots/es/diag-pretty-plots-07.html"
---
---
## Sesión de laboratorio:
### Ejercicio 1: Graficar algunas curvas interesantes.
**Instrucciones**
1. Carga a `QtCreator` el proyecto `prettyPlot`. Hay dos maneras de hacer esto:
* Utilizando la máquina virtual: Haz doble “click” en el archivo `prettyPlot.pro` que se encuentra en el directorio `/home/eip/labs/expressions-prettyplots` de la máquina virtual.
* Descargando la carpeta del proyecto de `Bitbucket`: Utiliza un terminal y escribe el commando `git clone http:/bitbucket.org/eip-uprrp/expressions-prettyplots` para descargar la carpeta `expressions-prettyplots` de `Bitbucket`. En esa carpeta, haz doble “click” en el archivo `prettyPlot.pro`.
2. Configura el proyecto y ejecuta el programa marcando la flecha verde en el menú de la izquierda de la interface de Qt Creator. El programa debe mostrar una ventana parecida a la Figura 3.
---
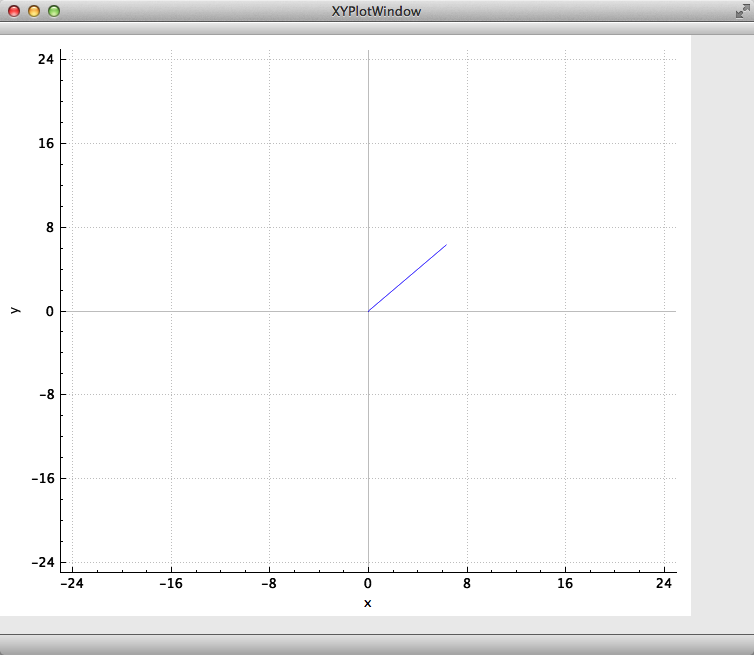
**Figura 3.** Segmento de línea desplegado por el programa PrettyPlot.
---
3. El archivo `main.cpp` (en Sources) contiene la función `main()` donde estarás añadiendo código. Abre ese archivo y estudia el código.
```cpp
QApplication a(argc, argv);
XYPlotWindow wLine;
XYPlotWindow wCircle;
XYPlotWindow wHeart;
XYPlotWindow wButterfly;
double y = 0.00;
double x = 0.00;
double increment = 0.01;
for (double t = 0; t < 2*M_PI; t = t + increment) {
// parametric equations
x = t;
y = t;
// add x and y as a point in the graph
wLine.AddPointToGraph(x,y);
}
// After all the points have been added, plot and show the graph
wLine.Plot();
wLine.show();
```
La línea `XYPlotWindow wLine;` crea el objeto `wLine` que será la ventana en donde se dibujará una gráfica, en este caso la gráfica de un segmento. Observa el ciclo `for`. En este ciclo se genera una serie de valores para $$t$$ y se computa un valor de $$x$$ y $$y$$ para cada valor de $$t$$. Cada par ordenado $$(x,y)$$ es añadido a la gráfica del segmento por el método `AddPointToGraph(x,y)`. Luego del ciclo se invoca el método `Plot()`, que "dibuja" los puntos, y el método `show()`, que muestra la gráfica. Los *métodos* son funciones que nos permiten trabajar con los datos de los objetos. Nota que cada uno de los métodos se escribe luego de `wLine`, seguido de un punto. En una experiencia de laboratorio posterior aprenderás más sobre objetos y practicarás cómo crearlos e invocar sus métodos.
Las expresiones que tiene tu programa para $$x$$ y $$y$$ son ecuaciones paramétricas para la línea que pasa por el origen y tiene el mismo valor para las coordenadas en $$x$$ y $$y$$. Explica por qué la línea solo va desde 0 hasta aproximadamente 6.
4. Ahora escribirás el código necesario para graficar un círculo. La línea `XYPlotWindow wCircle;` crea el objeto `wCircle` para la ventana donde se graficará el círculo. Usando como inspiración el código para graficar el segmento, escribe el código necesario para que tu programa grafique un círculo de radio 3 con centro en el origen. Ejecuta tu programa y, si es necesario, modifica el código hasta que obtengas la gráfica correcta. Recuerda que el círculo debe graficarse dentro del objeto `wCircle`. Por esto, al invocar los métodos `AddPointToGraph(x,y)`, `Plot` y `show`, éstos deben ser precedidos por `wCircle`, por ejemplo, `wCircle.show()`.
5. Tu próxima tarea es graficar una curva cuyas ecuaciones paramétricas son:
$$x=16 \sin^3(t)$$
$$y=13 \cos(t) - 5 \cos(2t) - 2 \cos(3t) - \cos(4t)-3.$$
Si implementas las expresiones correctamente debes ver la imagen de un corazón. Esta gráfica debe haber sido obtenida dentro de un objeto `XYPlotWindow` llamado `wHeart`.
6. Ahora graficarás una curva cuyas ecuaciones paramétricas son:
$$x=5\cos(t) \left[ \sin^2(1.2t) + \cos^3(6t) \right]$$
$$y= 10\sin(t) \left[ \sin^2(1.2t) + \cos^3(6t) \right].$$
Observa que ambas expresiones son casi iguales, excepto que una comienza con $$5\cos(t)$$ y la otra con $$10\sin(t)$$. En lugar de realizar el cómputo de $$ \sin^2(1.2t) + \cos^3(6t)$$ dos veces, puedes asignar su valor a otra variable $$q$$ y realizar el cómputo así:
$$q = \sin^2(1.2t) + \cos^3(6t)$$
$$x = 5 \cos(t)(q)$$
$$y = 10 \sin(t)(q).$$
Implementa las expresiones de arriba, cambia la condición de terminación del `for` a `t < 16*M_PI` y observa la gráfica que resulta. Se supone que parezca una mariposa. Esta gráfica debe haber sido obtenida dentro de un objeto `XYPlotWindow` llamado `wButterfly`.
En [2] y [3] puedes encontrar otras ecuaciones paramétricas de otras curvas interesantes.
### Ejercicio 2: Calcular el promedio de notas
En este ejercicio escribirás un programa para obtener el promedio de puntos para la nota (GPA, por sus siglas en inglés) de un estudiante. Supón que todos los cursos en la Universidad de Yauco son de $$3$$ créditos y que las notas tienen las siguientes puntuaciones: $$A = 4$$ puntos por crédito; $$B = 3$$ puntos por crédito; $$C = 2$$ puntos por crédito; $$D = 1$$ punto por crédito y $$F = 0$$ puntos por crédito.
**Instrucciones**
1. Crea un nuevo proyecto "Non-Qt" llamado Promedio. Tu función `main()` contendrá el código necesario para pedirle al usuario el número de A's, B's, C's, D's y F's obtenidas por el estudiante y computar el promedio de puntos para la nota (GPA por sus siglas en inglés).
2. Tu código debe definir las **constantes** $$A=4, B=3, C=2, D=1, F=0$$ para la puntuación de las notas, y pedirle al usuario que entre los valores para las variables $$NumA$$, $$NumB$$, $$NumC$$, $$NumD$$, $$NumF$$. La variable $$NumA$$ representará el número de cursos en los que el estudiante obtuvo $$A$$, $$NumB$$ representará el número de cursos en los que el estudiante obtuvo $$B$$, etc. El programa debe desplegar el GPA del estudiante en una escala de 0 a 4 puntos.
**Ayudas:**
a. El promedio se obtiene sumando las puntuaciones correspondientes a las notas obtenidas (por ejemplo, una A en un curso de 3 créditos tiene una puntuación de 12), y dividiendo esa suma por el número total de créditos.
b. Recuerda que, en C++, si divides dos números enteros el resultado se "truncará" y será un número entero. Utiliza "type casting": `static_cast(expresión)` para resolver este problema.
3. Verifica tu programa calculando el promedio de un estudiante que tenga dos A y dos B; ¿qué promedio tendría este estudiante? Cuando tu programa esté correcto, guarda el archivo `main.cpp`.
---
---
## Entregas
1. Usa "Entrega 1" en Moodle para entregar el archivo `main.cpp` que contiene el código con las ecuaciones paramétricas de las gráficas del círculo, el corazón y la mariposa. Recuerda utilizar buenas prácticas de programación, incluir el nombre de los programadores y documentar tu programa.
2. Usa "Entrega 2" en Moodle para entregar el archivo `main.cpp` que contiene el código para computar el promedio. Recuerda seguir las instrucciones en el uso de nombres y tipos para las variables, incluir el nombre de los programadores, documentar tu programa y utilizar buenas prácticas de programación.
##Referencias:
[1] http://mathworld.wolfram.com/ParametricEquations.html
[2] http://paulbourke.net/geometry/butterfly/
[3] http://en.wikipedia.org/wiki/Parametric_equation