# Arithmetic Expressions - Quadratic Frog



[verano 2016 - Coralys - Ive - Coralys]
Arithmetic expressions are an essential part of almost any algorithm that solves a useful problem. Therefore, a basic skill in any computer programming language is to implement arithmetic expressions correctly. In this laboratory experience you will practice the implementation of arithmetic expressions in C++ by writing equations for the quadratic formula and completing the code for a game in which a frog jumps from leaf to leaf.
## Objectives:
1. Implement arithmetic expressions in C++ to produce the graphs that will define the trajectory of the frog's jump in the game.
2. Use constant variables adequately.
3. Define variables using adequate data types.
4. Cast a data value to another type when necessary.
## Pre-Lab:
Before you get to the laboratory you should have:
1. Reviewed the following concepts:
a. Implementing arithmetic expressions in C++
b. Basic data types in C++ (int, float, double)
c. Using "type casting" to cast the value of variables to other data types within expressions
d. Using arithmetic functions and constants from the `cmath` library
e. Quadratic equations and their graphs
2. Studied the concepts and instructions for the laboratory session.
3. Taken the Pre-Lab quiz, available in Moodle.
---
---
## Quadratic Formula
A *quadratic equation* has the form
$$y = a x^2+ b x + c,$$
where $$a, b, c$$ are real numbers and $$a\not=0$$. The graph of a quadratic equation is a *parabola* that opens up if $$a > 0$$ and opens down if $$a < 0$$.
A graph intersects the $$x$$-axis when $$ y = 0 $$ . Therefore, if a parabola intersects the $$x$$-axis, the intersects are given by the real solutions to the equation
$$0 = a x^2 + b x + c.$$
The solutions to the previous equation can be obtained using the *quadratic formula*:
$$x=\frac{-b±\sqrt{b^2-4ac}}{2a}.$$
Note that if the *discriminant* $$b^2-4ac$$ of the quadratic formula is negative, the values of $$x$$ are complex numbers and are not plotted in the Cartesian plane. Therefore, if the discriminant is negative, the parabola does not intersect the $$x$$-axis. If the discriminant is equal to $$0$$, then the parabola intersects the $$x$$-axis in only one point (only the vertex touches the $$x$$-axis).
If the discriminant is positive, the quadratic formula gives two solutions to the equation $$0 = a x^2 + b x + c$$ and these solutions are the intersects in the $$x$$-axis. For example, suppose that the quadratic formula gives two values:
$$ x = x_1 $$
$$ x = x_2 $$
Then,
$$a x^2 + b x + c = a(x-x_1)(x-x_2),$$
where $$x_1$$ and $$x_2$$ are the intersects in the $$x$$-axis. If $$a<0$$, the graph of the parabola will be similar to the one in Figure 1.
---
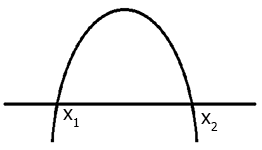
Figure 1. Parabola that opens down and intersects the $$x$$-axis in $$x_1$$ and $$x_2$$.
---
Note that the equation
$$y=-(x-x_1)(x-x_2)$$
is a quadratic equation and its parabola opens down and intersects the $$x$$-axis in $$x_1$$ and $$x_2$$. For example, the equation
$$y=-(x+2)(x-3)=-x^2+x+6$$
is a quadratic equation with a parabola that opens down and intersects the $$x$$-axis at $$x_1=-2$$ and $$x_2=3$$. Note that, in this equation, the values for $$a, b, c$$ are $$a=-1, \ b=1, \ c=6$$.
---
---
!INCLUDE "../../eip-diagnostic/quadratic-frog/en/diag-quadratic-frog-01.html"
!INCLUDE "../../eip-diagnostic/quadratic-frog/en/diag-quadratic-frog-08.html"
!INCLUDE "../../eip-diagnostic/quadratic-frog/en/diag-quadratic-frog-09.html"
---
---
## Laboratory session:
### Exercise 1 - Implement the quadratic formula
In this exercise you will implement the quadratic formula to complete a game in which a frog leaps from one leaf to another. You will assume that the leaves are in the $$x$$-axis and that the leap is determined by a parabola that opens down. If you want the frog to leap from leaf to leaf, you must find a quadratic equation with a parabola that opens down and intersects the $$x$$-axis in the places where the leaves are located. Your task is to write the equations for the quadratic formula.
#### Instructions
1. Load the project `QuadraticFrog` into `QtCreator`. There are two ways to do this:
* Using the virtual machine: Double click the file `QuadraticFrog.pro` located in the folder `home/eip/labs/expressions-quadraticFrog` of your virtual machine.
* Downloading the project's folder from `Bitbucket`: Use a terminal and write the command `git clone http://bitbucket.org/eip-uprrp/expressions-quadraticfrog` to download the folder `expressions-quadraticfrog` from `Bitbucket`. Double click the file `QuadraticFrog.pro`located in the folder that you downloaded to your computer.
2. Configure the project and run the program by clicking the green arrow in the menu on the left side of the Qt Creator window. The program will display a message saying that the quadratic formula is wrong. This happens because the program has testing instructions that verify that the code implementation is correct. Your program is missing the code for the quadratic formula, so this is why the message is displayed.
3. You will write the equations for the quadratic formula in the file `QuadraticFormula.cpp` (in `Sources`). In the function `QuadraticPlus` add the equation
$$result=\frac{-b+\sqrt{b^2-4ac}}{2a},$$
and in the function `QuadraticMinus` add the equation
$$result=\frac{-b-\sqrt{b^2-4ac}}{2a}.$$
The other files of the project have code that will test your equations by evaluating several choices for $$a, b, c$$ and verifying that the equations produce the expected result. Code validation is an important part of software development.
4. Run the program by clicking the green arrow in the menu on the left side of the Qt Creator window. If your equations are implemented correctly, you should obtain a window similar to the one in Figure 2.
---
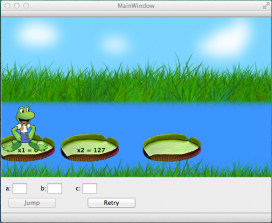
Figure 2. Window of the game *Quadratic Frog*.
---
5. To play, the frog should leap from one leaf to another. Note that the leaves have values for $$x_1$$ and $$x_2$$. These values represent the intersects of the parabola with the $$x$$-axis. You should input the values for the coefficients $$a, b, c$$ of the quadratic equation so that its graph is a parabola that opens down and intersects the $$x$$-axis in the values $$x_1, x_2$$ shown in the leaves. You can obtain these values noting that $$a x^2 + b x + c = a(x-x_1)(x-x_2),$$ as in the explanation above.
### Exercise 2 - Write a program to obtain a student's grade point average (GPA)
Suppose that all courses in Yauco's University are 3 credits each and have the following point values: $$A = 4$$ points per credit; $$B = 3$$ points per credit; $$C = 2$$ points per credit; $$D = 1$$ point per credit and $$F = 0$$ points per credit.
#### Instructions
1. Start a new "Non-Qt" project called "Average". Your `main()` function will have the necessary code to ask the user for the number of A's, B's, C's, D's and F's obtained and compute the grade point average (GPA).
2. Your code should define the constants $$A=4, B=3, C=2, D=1, F=0$$ for the points per credit, and ask the user to input the values for the variables $$NumA$$, $$NumB$$, $$NumC$$, $$NumD$$, $$NumF$$. The variable $$NumA$$ represents the number of courses in which the student obtained A, $$NumB$$ represents the number of courses in which the student obtained B, etc. The program should display the GPA using the 0-4 point scale.
**Hints:**
1. You can obtain the GPA by adding the credit points corresponding to the grades (for example, an A in a 3 credit course has a value of 12 points), and dividing this sum by the total number of credits.
2. Remember that, in C++, when both operands in the division are integers, the result will also be an integer; the remainder will be discarded. Use "type casting": `static_cast(expression)` to solve this problem.
3. Verify your program by computing the GPA of a student that has two A's and 2 B's; what is the grade of this student, A or B (A goes from 3.5 to 4 points)? When your program is correct, save the `main.cpp` file.
---
---
## Deliverables
1. Use "Deliverable 1' in Moodle to submit the file `QuadraticFormula.cpp` containing the code with the functions `QuadraticPlus` and `QuadraticMinus`. Remember to use good programming practices, include the names of the programmers, and document your program.
2. Use "Deliverable 2" to submit the file `main.cpp` with the code to compute the grade point average. Remember to follow the instructions regarding the names and types of the variables, to include the names of the programmers, to document your program and to use good programming practices.