EIP
/
expressions-quadraticfrog
Obserwuj 2
Gwiazdka 0
Forkuj 0
Kod Problemy 0 Pull Requests 0 Wydania 0 Wiki Aktywność
Brak opisu
36 Commity
3 Gałęzie
Drzewo: fadea76e93
Gałęzie Tagi
${ item.name }
Utwórz gałąź ${ searchTerm }
z 'fadea76e93'
${ noResults }
expressions-quadraticfrog/README-es.md

README-es.md 9.4KB
Historia Czysty

Expresiones aritméticas - Sapo Cuadrático

main1.png main2.png main4.png

[verano 2016 - Coralys - Ive - Coralys]

Las expresiones aritméticas son parte esencial de casi cualquier algoritmo que resuelve un problema útil. Por lo tanto, implementar expresiones aritméticas correctamente es una destreza básica en cualquier lenguaje de programación de computadoras. En esta experiencia de laboratorio practicarás la implementación de expresiones aritméticas en C++, escribiendo ecuaciones para la fórmula cuadrática y así, completar el código para un juego en el que un sapito brinca de una hoja a otra.

Objetivos:

  1. Implementar expresiones aritméticas en C++ para definir la trayectoria del brinco del sapito en el juego.
  2. Utilizar variables constantes adecuadamente.
  3. Definir variables utilizando tipos de datos adecuados.
  4. Convertir el valor de un dato a otro tipo cuando sea necesario.

Pre-Lab:

Antes de llegar al laboratorio debes:

  1. Haber repasado los siguientes conceptos:

    a. La implementación de expresiones aritméticas en C++

    b. Los tipos de datos básicos de C++ (int, float, double, char)

    c. El uso de “type casting” para covertir el valor de una variable a otro tipo dato dentro de expresiones

    d. Utilizar funciones y constantes aritméticas de la biblioteca cmath

    e. Ecuaciones cuadráticas y sus gráficas.

  2. Haber estudiado los conceptos e instrucciones para la sesión de laboratorio.

  3. Haber tomado el quiz Pre-Lab disponible en Moodle.

Fórmula cuadrática

Una ecuación cuadrática tiene la forma

$$y = a x^2+ b x + c,$$

donde $$a, b, c$$ son números reales y $$a\not=0$$. La gráfica de una ecuación cuadrática es una parábola que abre hacia arriba si $$a > 0$$ y abre hacia abajo si $$a < 0$$.

Una gráfica interseca el eje de $$x$$ cuando $$ y = 0 $$ . Por lo tanto, si una parábola interseca el eje de $$x$$, los intersectos están dados por las soluciones reales de la ecuación

$$0 = a x^2 + b x + c.$$

Las soluciones a la ecuación anterior se pueden obtener utilizando la fórmula cuadrática:

$$x = \frac{-b±\sqrt{b^2-4ac}}{2a}.$$

Nota que si el discriminante $$b^2-4ac$$ de la fórmula cuadrática es negativo, los valores de $$x$$ serán números imaginarios y no se pueden graficar en el plano cartesiano porque los puntos $$(x,y)$$ en este plano tienen coordenadas que son números reales. Por lo tanto, si el discriminante es negativo, la parábola no interseca el eje de $$x$$. Si el discriminate es igual a $$0$$, entonces la parábola interseca el eje de $$x$$ en un solo punto (solo el vértice toca el eje de $$x$$).

Si el discriminante es positivo, la fórmula cuadrática nos da dos soluciones a la ecuación $$0 = a x^2 + b x + c$$ y estas soluciones son los intersectos en el eje de $$x$$. Por ejemplo, supón que la fórmula cuadrática nos da dos valores:

$$x = x_1 $$ $$x = x_2 $$

Entonces,

$$a x^2 + b x + c = a(x-x_1)(x-x_2),$$

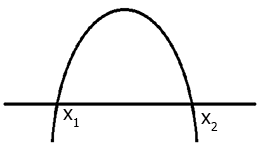
donde $$x_1$$ y $$x_2$$ son los cortes en el eje de $$x$$. Si $$a<0$$, la gráfica de la parábola será similar a la de la Figura 1.

parabola.png

Figura 1. Parábola que abre hacia abajo e interseca el eje de $$x$$ en $$x_1$$ y $$x_2$$.

Nota que la ecuación

$$y = -(x-x_1)(x-x_2)$$

es una ecuación cuadrática cuya parábola abre hacia abajo e interseca el eje de $$x$$ en $$x_1$$ y $$x_2$$. Por ejemplo, la ecuación

$$y = -(x+2)(x-3)=-x^2+x+6$$

es una ecuación cuadrática cuya parábola abre hacia abajo e interseca el eje de $$x$$ en $$x_1=-2$$ y $$x_2=3$$. Nota que, en esta ecuación, los valores de $$a,b,c$$ son $$a=-1, \ b=1, \ c=6$$.

!INCLUDE “../../eip-diagnostic/quadratic-frog/es/diag-quadratic-frog-01.html”

!INCLUDE “../../eip-diagnostic/quadratic-frog/es/diag-quadratic-frog-08.html”

!INCLUDE “../../eip-diagnostic/quadratic-frog/es/diag-quadratic-frog-09.html”

Sesión de laboratorio:

Ejercicio 1 - Implementar la fórmula cuadrática

En este ejercicio implementarás la fórmula cuadrática para completar un juego en el que un sapito brinca de una hoja a otra. Asumirás que las hojas están localizadas sobre el eje de $$x$$ y que el brinco del sapito estará determinado por una parábola que abre hacia abajo. Si quieres que el sapito brinque de hoja a hoja, debes hayar una ecuación cuadrática cuya parábola abra hacia abajo e interseque el eje de $$x$$ en los lugares donde están localizadas las hojas. Tu tarea es escribir las ecuaciones para la fórmula cuadrática.

Instrucciones

  1. Carga a Qt el proyecto QuadraticFrog. Hay dos maneras de hacer esto:

    • Utilizando la máquina virtual: Haz doble “click” en el archivo QuadraticFrog.pro que se encuentra en el directorio home/eip/labs/expressions-quadraticfrog de la máquina virtual.

    • Descargando la carpeta del proyecto de Bitbucket: Utiliza un terminal y escribe el comando git clone http://bitbucket.org/eip-uprrp/expressions-quadraticfrog para descargar la carpeta expressions-quadraticfrog. En esa carpeta, haz doble “click” en el archivo QuadraticFrog.pro.

  2. Configura el proyecto y ejecuta el programa marcando la flecha verde en el menú de la izquierda de la ventana de Qt Creator. El programa te dará un mensaje que dice que la fórmula cuadrática está mal escrita. Esto sucede porque el programa tiene instrucciones que prueban el programa y verifican que la implementación del código esté correcta. Tu programa aún no tiene las instrucciones para evaluar la fórmula cuadrática y por esto sale el mensaje.

  3. En el archivo QuadraticFormula.cpp (en Sources) escribirás las ecuaciones para la fórmula cuadrática. En la función QuadraticPlus añade la ecuación

    $$result = \frac{-b+\sqrt{b^2-4ac}}{2a},$$

    y en la función QuadraticMinus añade la ecuación

    $$result = \frac{-b-\sqrt{b^2-4ac}}{2a}.$$

    Los otros archivos del proyecto tienen código que hará pruebas a las ecuaciones que escribiste, evaluando varios valores para $$a, b ,c$$ y verificando que el resultado que producen las ecuaciones es el esperado. La validación del código de un programa es una parte importante del desarrollo de programas y proyectos.

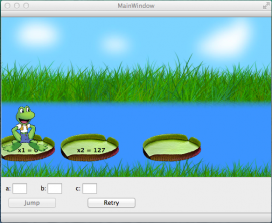
  4. Ejecuta el programa marcando el botón verde en el menú de la izquierda. Si las ecuaciones que escribiste están correctas, deberá aparecer una ventana parecida a la Figura 2.

    figure2.png

    Figura 2. Ventana del juego Sapo Cuadrático.

  5. Para jugar, el sapito deberá brincar de una hoja a otra. Nota que las hojas tienen valores para $$x_1$$ y $$x_2$$. Estos valores representan los intersectos en el eje de $$x$$ de la parábola. Debes entrar los valores para los coeficientes $$a,b,c$$ de la ecuación cuadrática de modo que la gráfica sea una parábola que abra hacia abajo e interseque el eje de $$x$$ en los valores $$x_1, x_2$$ que salen en las hojas. Puedes obtener los valores de $$a,b,c$$ notando que $$a x^2 + b x + c = a(x-x_1)(x-x_2),$$ como en la explicación de arriba.

Ejercicio 2 - Escribir un programa para obtener el promedio notas

Supón que todos los cursos en la Universidad de Yauco son de 3 créditos y que las notas tienen las siguientes puntuaciones: $$A = 4$$ puntos por crédito; $$B = 3$$ puntos por crédito; $$C = 2$$ puntos por crédito; $$D = 1$$ punto por crédito y $$F = 0$$ puntos por crédito.

Instrucciones

  1. Crea un nuevo proyecto “Non-Qt” llamado Promedio. Tu función main() tendrá el código necesario para pedirle al usuario el número de A’s, B’s, C’s, D’s y F’s obtenidas por el estudiante y computar el promedio de puntos para la nota (GPA por sus siglas en inglés).

  2. Tu código debe definir las constantes $$A=4, B=3, C=2, D=1, F=0$$ para la puntuación de las notas, y pedirle al usuario que entre los valores para las variables $$NumA$$, $$NumB$$, $$NumC$$, $$NumD$$, $$NumF$$. La variable $$NumA$$ representará el número de cursos en los que el estudiante obtuvo $$A$$, $$NumB$$ representará el número de cursos en los que el estudiante obtuvo $$B$$, etc. El programa debe desplegar el GPA del estudiante en una escala de 0 a 4 puntos.

    Ayudas:

    1. El promedio se obtiene sumando las puntuaciones correspondientes a las notas obtenidas (por ejemplo, una A en un curso de 3 créditos tiene una puntuación de 12), y dividiendo esa suma por el número total de créditos.

    2. Recuerda que, en C++, si divides dos números enteros el resultado se “truncará” y será un número entero. Utiliza “type casting”: static_cast<tipo>(expresión) para resolver este problema.

  3. Verifica tu programa calculando el promedio de un estudiante que tenga dos A y dos B; ¿qué nota tendría este estudiante, A o B (la A va desde 3.5 a 4.0)?. Cuando tu programa esté correcto, guarda el archivo main.cpp.

Entregas

  1. Utiliza “Entrega 1” en Moodle para entregar el archivo QuadraticFormula.cpp que contiene las funciones QuadraticPlus y QuadraticMinus. Recuerda utilizar buenas prácticas de programación, incluye el nombre de los programadores y documenta tu programa.

  2. Usa “Entrega 2” en Moodle para entregar el archivo main.cpp que contiene el código para computar el promedio. Recuerda seguir las instrucciones en el uso de nombres y tipos para las variables, incluir el nombre de los programadores, documentar tu programa y utilizar buenas prácticas de programación.