No Description

Utilizando funciones en C++ - Gráficas Bonitas

[Version 2016- Tatiana]

Una buena manera de organizar y estructurar los programas de computadoras es dividiéndolos en partes más pequeñas utilizando funciones. Cada función realiza una tarea específica del problema que estamos resolviendo.

Haz visto que todos los programas en C++ deben contener la función main que es donde comienza el programa. Probablemente ya has utilizado funciones como pow, sin, cos o sqrt de la biblioteca de matemática cmath. Dado que en casi todas las experiencias de laboratorio futuras estarás utilizando funciones que ya han sido creadas, necesitas aprender cómo trabajar con ellas. Más adelante aprenderás cómo diseñarlas y validarlas. En esta experiencia de laboratorio invocarás y definirás funciones que calculan las coordenadas de los puntos de las gráficas de algunas curvas. También practicarás la implementación de expresiones aritméticas en C++.

Objetivos:

Identificar las partes de una función: tipo, nombre, lista de parámetros y cuerpo de la función.
Invocar funciones ya creadas enviando argumentos por valor (“pass by value”) y por referencia (“pass by reference”).
Implementar una función sobrecargada simple.
Implementar funciones simples que utilicen parámetros por referencia.
Implementar expresiones aritméticas en C++

Pre-Lab:

Antes de llegar al laboratorio debes haber:

Repasado los siguientes conceptos:

a. los elementos básicos de la definición de una función en C++.

b. la manera de invocar funciones en C++.

c. la diferencia entre parámetros pasados por valor y por referencia.

d. cómo devolver el resultado de una función.

e. implementar expresiones aritméticas en C++.

f. utilizar funciones y constantes aritméticas de la biblioteca cmath.

g. la ecuación y gráfica de un círculo.
Estudiado los conceptos e instrucciones para la sesión de laboratorio.
Tomado el quiz Pre-Lab que se encuentra en Moodle.

Funciones

En matemática, una función $$f$$ es una regla que se usa para asignar a cada elemento $$x$$ de un conjunto llamado dominio, uno (y solo un) elemento $$y$$ de un conjunto llamado campo de valores. Por lo general, esa regla se representa como una ecuación, $$y=f(x)$$. La variable $$x$$ es el parámetro de la función y la variable $$y$$ contendrá el resultado de la función. Una función puede tener más de un parámetro pero solo un resultado. Por ejemplo, una función puede tener la forma $$y=f(x_1,x_2)$$ en donde hay dos parámetros y para cada par $$(a,b)$$ que se use como argumento de la función, la función tendrá un solo valor de $$y=f(a,b)$$. El dominio de la función te dice el tipo de valor que debe tener el parámetro y el campo de valores el tipo de valor que tendrá el resultado que devuelve la función.

Las funciones en lenguajes de programación de computadoras son similares. Una función tiene una serie de instrucciones que toman los valores asignados a los parámetros y realiza alguna tarea. En C++ y en algunos otros lenguajes de programación, las funciones pueden devolver a lo sumo un resultado, tal y como sucede en matemáticas. La única diferencia es que una función en programación puede que no devuelva un valor (en este caso la función se declara void). Si la función va a devolver algún valor, se hace con la instrucción return. Al igual que en matemática tienes que especificar el dominio y el campo de valores, en programación tienes que especificar los tipos de valores que tienen los parámetros y el resultado que devuelve la función; esto lo haces al declarar la función.

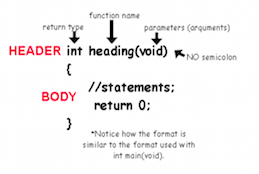
Encabezado de una función:

La primera oración de una función se llama el encabezado y su estructura es como sigue:

tipo nombre(tipo parámetro_1, ..., tipo parámetro_n)

Por ejemplo,

int ejemplo(int var1, float var2, char &var3)

sería el encabezado de la función llamada ejemplo, que devuelve un valor entero. La función recibe como argumentos un valor entero (y guardará una copia en var1), un valor de tipo float (y guardará una copia en var2) y la referencia a una variable de tipo char que se guardará en la variable de referencia var3. Nota que var3 tiene el signo & antes del nombre de la variable. Esto indica que var3 contendrá la referencia a un carácter.

Invocación

Si queremos guardar el valor del resultado de la función ejemplo en la variable resultado (que deberá ser de tipo entero), invocamos la función pasando argumentos de manera similar a:

resultado = ejemplo(2, 3.5, unCar);

Nota que al invocar funciones no incluyes el tipo de las variables en los argumentos como en la definición de la función ejemplo. El tercer parámetro &var3 es una variable de referencia, esto significa que lo que se está enviando en el tercer argumento de la invocación es una referencia a la variable unCar. Los cambios que se hagan en la variable var3 están cambiando el contenido de la variable unCar.

También puedes usar el resultado de la función sin tener que guardarlo en una variable. Por ejemplo puedes imprimirlo:

cout << "El resultado de la función ejemplo es:" << ejemplo(2, 3.5, unCar);

o utilizarlo en una expresión aritmética:

y = 3 + ejemplo(2, 3.5, unCar);

Funciones sobrecargadas (‘overloaded’)

Las funciones sobrecargadas son funciones que poseen el mismo nombre, pero tienen firmas diferentes.

La firma de una función se compone del nombre de la función, y los tipos de parámetros que recibe, pero no incluye el tipo que devuelve.

Los siguientes prototipos de funciones tienen la misma firma:

int ejemplo(int, int) ;
void ejemplo(int, int) ;
string ejemplo(int, int) ;

Nota que todas tienen el mismo nombre, ejemplo, y reciben la misma cantidad de parámetros del mismo tipo (int, int).

Los siguientes prototipos de funciones tienen firmas diferentes:

int ejemplo(int) ;
int olpmeje(int) ;

Nota que a pesar de que las funciones tienen la misma cantidad de parámetros con mismo tipo int, el nombre de las funciones es distinto.

Los siguientes prototipos de funciones son versiones sobrecargadas de la función ejemplo:

int ejemplo(int) ;
void ejemplo(char) ;
int ejemplo(int, int) ;
int ejemplo(char, int) ;
int ejemplo(int, char) ;

Todas las funciones de arriba tienen el mismo nombre, ejemplo, pero distintos parámetros. La primera y segunda función tienen la misma cantidad de parámetros, pero los argumentos son de distintos tipos. La cuarta y quinta función tienen argumentos de tipo char e int, pero en cada caso están en distinto orden.

En este último ejemplo la función ejemplo es sobrecargada ya que hay cinco funciones con firma distinta pero con el mismo nombre.

Valores predeterminados

Se pueden asignar valores predeterminados (“default”) a los parámetros de las funciones comenzando desde el parámetro que está más a la derecha. No hay que inicializar todos los parámetros pero los que se inicializan deben ser consecutivos: no se puede dejar parámetros sin inicializar entre dos parámetros que estén inicializados. Esto permite la invocación de la función sin tener que enviar los valores en las posiciones que corresponden a parámetros inicializados.

Ejemplos de encabezados de funciones e invocaciones válidas:

Encabezado: int ejemplo(int var1, float var2, int var3 = 10)

Invocaciones:

a. ejemplo(5, 3.3, 12) Esta invocación asigna el valor 5 a var1, el valor 3.3 a var2, y el valor 12 a var3.

b. ejemplo(5, 3.3) Esta invocación envía valores para los primeros dos parámetros y el valor del último parámetro será el valor predeterminado asignado en el encabezado. Esto es, los valores de las variables en la función serán: var1 tendrá 5, var2 tendrá 3.3, y var3 tendrá 10.
Encabezado: int ejemplo(int var1, float var2=5.0, int var3 = 10)

Invocaciones:

a. `ejemplo(5, 3.3, 12)` Esta invocación asigna el valor 5 a `var1`, el valor 3.3 a `var2`, y el valor 12 a  `var3`.

b. `ejemplo(5, 3.3)` En esta invocación solo se envían valores para los primeros dos parámetros, y el valor del último parámetro es el valor predeterminado.  Esto es, el valor de `var1` dentro de la función será 5, el de `var2` será 3.3 y el de `var3` será 10.

c. `ejemplo(5)` En esta invocación solo se envía valor para el primer parámetro, y los últimos dos parámetros tienen valores predetermiandos.  Esto es,  el valor de `var1` dentro de la función será 5, el de `var2` será 5.0 y el de `var3` será 10.

Ejemplo de un encabezado de funciones válido con invocaciones inválidas:

Encabezado: int ejemplo(int var1, float var2=5.0, int var3 = 10)

Invocación:

a. ejemplo(5, ,10) Esta invocación es inválida porque deja espacio vacío en el argumento del medio.

b. ejemplo() Esta invocación es inválida ya que var1 no estaba inicializada y no recibe ningún valor en la invocación. Una invocación válida para la función ejemplo necesita al menos un argumento (el primero).

Ejemplos de encabezados de funciones inválidos:

int ejemplo(int var1=1, float var2, int var3) Este encabezado es inválido porque los valores predeterminados sólo se pueden asignar comenzando por el parámetro que está más a la derecha.
int ejemplo(int var1=1, float var2, int var3=10) Este encabezado es inválido porque no se pueden poner parámetros sin valores en medio de parámetros con valores predeterminados. En este caso var2 no tiene valor pero var1 y var3 si tienen.

Ecuaciones paramétricas

Las ecuaciones paramétricas nos permiten representar una cantidad como función de una o más variables independientes llamadas parámetros. En muchas ocasiones resulta útil representar curvas utilizando un conjunto de ecuaciones paramétricas que expresan las coordenadas de los puntos de la curva como funciones de los parámetros. Por ejemplo, en tu curso de trigonometría debes haber estudiado que la ecuación de un círculo con radio $$r$$ y centro en el origen tiene una forma así:

$$x^2+y^2=r^2.$$

Los puntos $$(x,y)$$ que satisfacen esta ecuación son los puntos que forman el círculo de radio $$r$$ y su centro en el origen. Por ejemplo, el círculo con $$r=2$$ y centro en el origen tiene ecuación

$$x^2+y^2=4,$$

y sus puntos son los pares ordenados $$(x,y)$$ que satisfacen esa ecuación. Una forma paramétrica de expresar las coordenadas de los puntos del círculo con radio $$r$$ y centro en el origen es:

$$x=r \cos(t)$$

$$y=r \sin(t),$$

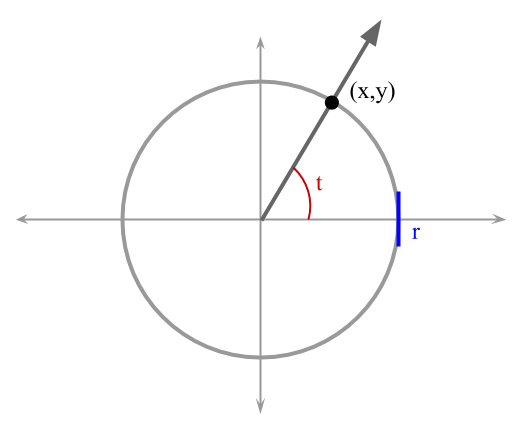
donde $$t$$ es un parámetro que corresponde a la medida (en radianes) del ángulo positivo con un lado inicial que coincide con la parte positiva del eje de $$x$$, y un lado terminal que contiene el punto $$(x,y)$$, como se muestra en la Figura 1.

Figura 1. Círculo con centro en el origen y radio $$r$$.

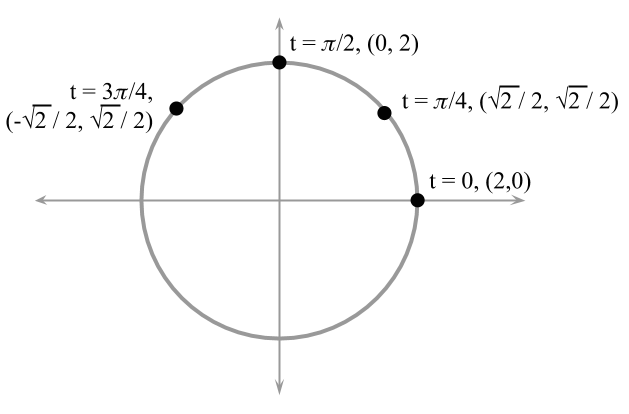
Para graficar una curva que está definida usando ecuaciones paramétricas, computamos los valores de $$x$$ y $$y$$ para un conjunto de valores del parámetro. Por ejemplo, la Figura 2 resalta los valores de $$t$$, $$(x,y)$$ para el círculo con $$r = 2$$.

Figura 2. Algunas coordenadas de los puntos $$(x,y)$$ del círculo con radio $$r=2$$ y centro en el origen.

!INCLUDE “../../eip-diagnostic/DVD/es/diag-dvd-01.html”

!INCLUDE “../../eip-diagnostic/DVD/es/diag-dvd-03.html”

!INCLUDE “../../eip-diagnostic/DVD/es/diag-dvd-11.html”

!INCLUDE “../../eip-diagnostic/DVD/es/diag-dvd-12.html”

Sesión de laboratorio:

En la introducción al tema de funciones viste que, tanto en matemáticas como en algunos lenguajes de programación, una función no puede devolver más de un resultado. En los ejercicios de esta experiencia de laboratorio practicarás cómo usar variables de referencia para poder obtener varios resultados de una función.

Ejercicio 1

En este ejercicio estudiarás la diferencia entre pase por valor y pase por referencia.

Instrucciones

Carga a QtCreator el proyecto prettyPlot. Hay dos maneras de hacer esto:

*Utilizando la máquina virtual: Haz doble “click” en el archivo `prettyPlot.pro` que se encuentra en el directorio `home/eip/labs/functions-prettyplots` de la máquina virtual.
*Descargando la carpeta de `Bitbucket`: Utiliza un terminal y escribe el comando `git clone http://bitbucket.org/eip-uprrp/functions-prettyplots` para descargar la carpeta `functions-prettyplots` de `Bitbucket`. En esa carpeta, haz doble “click” en el archivo `prettyPlot.pro`.

Carga a Qt Creator el proyecto prettyPlot haciendo doble “click” en el archivo prettyPlot.pro que se encuentra en la carpeta Documents/eip/functions-prettyplots de tu computadora.
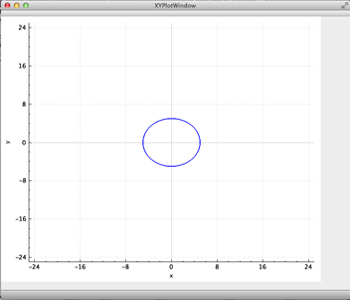
Configura el proyecto y ejecuta el programa marcando la flecha verde en el menú de la izquierda de la interface de QtCreator. El programa debe mostrar una ventana parecida a la Figura 3.

Figura 3. Gráfica de un círculo de radio 5 y centro en el origen desplegada por el programa PrettyPlot.

Abre el archivo main.cpp (en Sources). Estudia la función illustration y su invocación desde la función main. Nota que las variables argValue y argRef están inicializadas a 0 y que la invocación a illustration hace un pase por valor de argValue y un pase por referencia de argRef. Nota también que a los parámetros correspondientes en illustration se les asigna el valor 1.
```
void illustration(int paramValue, int &paramRef) {
    paramValue = 1;
    paramRef = 1;
    cout << endl << "The content of paramValue is: " << paramValue << endl
         << "The content of paramRef is: " << paramRef << endl;
}
```
Ejecuta el programa y observa lo que se despliega en la ventana Application Output. Nota la diferencia entre el contenido las variables argValue y argRef a pesar de que ambas tenían el mismo valor inicial y que a paramValue y paramRef se les asignó el mismo valor. Explica por qué el contenido de argValue no cambia, mientras que el contenido de argRef cambia de 0 a 1.

Ejercicio 2

En este ejercicio practicarás la creación de una función sobrecargada.

Instrucciones

Estudia el código de la función main() del archivo main.cpp. La línea XYPlotWindow wCircleR5; crea el objeto wCircleR5 que será la ventana en donde se dibujará una gráfica, en este caso la gráfica de un círculo de radio 5. De manera similar se crean los objetos wCircle y wButterfly. Observa el ciclo for. En este ciclo se genera una serie de valores para el ángulo $$t$$ y se invoca la función circle, pasándole el valor de $$t$$ y las referencias a $$x$$ y $$y$$. La función circle no devuelve valor pero, usando parámetros por referencia, calcula valores para las coordenadas $$xCoord$$ y $$yCoord$$ del círculo con centro en el origen y radio 5. Además, permite que la función main tenga esos valores en las variables x , y.
```
XYPlotWindow wCircleR5;
XYPlotWindow wCircle;
XYPlotWindow wButterfly;

double r;
double y = 0.00;
double x = 0.00;
double increment = 0.01;
int argValue=0, argRef=0;

// invoca la función illustration para ver los contenidos de la variable
// por valor y por referencia.

    illustration(argValue,argRef);
    cout << endl << "El contenido de argValue es: " << argValue << endl
         << "El contenido de argRef es: " << argRef << endl;

// repite por varios valores para el ángulo t
for (double t = 0; t < 16*M_PI; t = t + increment) {

    // invoca circle con el ángulo t y las variables de referencia x, y como argumentos
    circle(t,x,y);

    // añade el punto (x,y) a la gráfica del círculo
    wCircleR5.AddPointToGraph(x,y);
```
Luego de la invocación, cada par ordenado $$(x,y)$$ es añadido a la gráfica del círculo por el método AddPointToGraph(x,y). Luego del ciclo se invoca el método Plot(), que “dibuja” los puntos, y el método show(), que muestra la gráfica. Los métodos son funciones que nos permiten trabajar con los datos de los objetos. Nota que cada uno de los métodos se escribe luego de wCircleR5, seguido de un punto. En una experiencia de laboratorio posterior, aprenderás más sobre objetos y practicarás cómo crearlos e invocar sus métodos.

La función circle implementada en el programa es muy restrictiva ya que siempre calcula los valores para las coordenadas $$x$$ y $$y$$ del mismo círculo: el círculo con centro en el origen y radio 5.
Ahora crearás una función sobrecargada circle que reciba como argumentos el valor del ángulo $$t$$, la referencia a las variables $$x$$ y $$y$$, y el valor para el radio del círculo. Invoca desde main() la función sobrecargada circle que acabas de implementar para calcular los valores de las coordenadas $$x$$ y $$y$$ del círculo con radio 15 y dibujar su gráfica. Gráfica el círculo dentro del objeto wCircle. Para esto, debes invocar desde main() los métodos AddPointToGraph(x,y), Plot y show. Recuerda que éstos deben ser precedidos por wCircle, por ejemplo, wCircle.show().

Ejercicio 3

En este ejercicio implementarás otra función para calcular las coordenadas de los puntos de la gráfica de una curva.

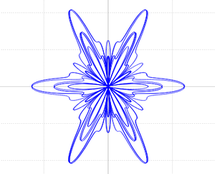
Instrucciones

Ahora crearás una función para calcular las coordenadas de los puntos de la gráfica que parece una mariposa. Las ecuaciones paramétricas para las coordenadas de los puntos de la gráfica están dadas por:

$$x=5\cos(t) \left[ \sin^2(1.2t) + \cos^3(6t) \right]$$

$$y= 10\sin(t) \left[ \sin^2(1.2t) + \cos^3(6t) \right].$$

Observa que ambas expresiones son casi iguales, excepto que una comienza con $$5\cos(t)$$ y la otra con $$10\sin(t)$$. En lugar de realizar el cómputo de $$ \sin^2(1.2t) + \cos^3(6t)$$ dos veces, puedes asignar su valor a otra variable $$q$$ y realizar el cómputo así:

$$q = \sin^2(1.2t) + \cos^3(6t)$$

$$x = 5 \cos(t)(q)$$

$$y = 10 \sin(t)(q).$$
Implementa la función butterfly utilizando las expresiones de arriba, invoca la función desde main() y observa la gráfica que resulta. Se supone que parezca una mariposa. Esta gráfica debe haber sido obtenida dentro de un objeto XYPlotWindow llamado wButterfly, invocando métodos de manera similar a como hiciste en el Ejercicio 2 para el círculo.

En [2] y [3] puedes encontrar otras ecuaciones paramétricas de otras curvas interesantes.

Entregas

Utiliza “Entrega” en Moodle para entregar el archivo main.cpp que contiene las funciones que implementaste, las invocaciones y cambios que hiciste en los ejercicios 2 y 3. Recuerda utilizar buenas prácticas de programación, incluir el nombre de los programadores y documentar tu programa.

Referencias

[1] http://mathbits.com/MathBits/CompSci/functions/UserDef.htm

[2] http://paulbourke.net/geometry/butterfly/

[3] http://en.wikipedia.org/wiki/Parametric_equation

README-es.md 19KB History Raw

Utilizando funciones en C++ - Gráficas Bonitas

Objetivos:

Pre-Lab:

Funciones

Encabezado de una función:

Invocación

Funciones sobrecargadas (‘overloaded’)

Valores predeterminados

Ecuaciones paramétricas

Sesión de laboratorio:

Ejercicio 1

Ejercicio 2

Ejercicio 3

Entregas

Referencias

README-es.md 19KB

History Raw