# Estructuras de Repetición - Pintar en Cuadrícula

[Version 2016-05-10]
La recursión es una técnica muy utilizada en programación. Con esta técnica se resuelven problemas resolviendo un problema similar pero para casos más pequeños. Podemos construir conjuntos de objetos o procesos utilizando *reglas recursivas* y *valores iniciales*. Las *funciones recursivas* son funciones que se auto-invocan, utilizando cada vez conjuntos o elementos más pequeños, hasta llegar a un punto en donde se utiliza la condición inicial en lugar de auto-invocarse. En esta experiencia de laboratorio implementarás algunas herramientas para dibujar y practicarás el uso de funciones recursivas para rellenar de color algunas figuras.
## Objetivos:
1. Definir e implementar funciones recursivas.
2. Practicar el uso de estructuras de repetición.
Esta experiencia de laboratorio es una adaptación de la asignación *GridPlotter* presentada por Alyce Brady y Pamela Cutter en [1]. La implementación de la cuadrícula y la capacidad de pintar en ella fue presentada por Sacha Schutz en [2] pero fue arreglada, modificada y adaptada para esta experiencia de laboratorio.
## Pre-Lab:
Antes de llegar al laboratorio debes haber:
1. Repasado los conceptos relacionados a funciones recursivas.
2. Estudiado los conceptos e instrucciones para la sesión de laboratorio.
3. Tomado el quiz Pre-Lab que se encuentra en Moodle.
---
---
## Aplicaciones para dibujar
Probablemente muchos usuarios del sistema operativo Windows (¡quizás todos!) han usado el programa *Paint*, que es una aplicación simple para dibujar. En ese programado, al igual que en muchos otros programados para dibujar, hay varias herramientas (por ejemplo el lápiz, el cubo de pintura, la línea) que le permiten al usuario dibujar en el área de distintas maneras.
En esta experiencia de laboratorio haremos funcionar algunas de esas herramientas: cuadrado, círculo, triángulo, y algunas líneas especiales ... ¡no te asustes!, lo haremos de una manera simple.
El dibujo se hará sobre una cuadrilla. Las herramientas se utilizarán marcando cualquier celda en la cuadrilla y, desde ese punto, las celdas necesarias para hacer la figura se pintarán. Por ejemplo, si seleccionamos la herramienta de línea vertical y marcamos la celda en posición *(2,3)*, una línea vertical se dibujará en todas las celdas de la columna 2. Esto es, se marcarán todas las celdas en posición $(2,y)$ para todas las $y$ de la cuadrilla.
---
---
## Coordenadas en `Qt`:
* El sistema de coordenadas en `Qt` funciona un poco diferente, como muestra la Figura 1. Las entradas van de izquierda a derecha, desde 0 hasta un ancho máximo, y desde arriba hasta abajo, desde 0 hasta una altura máxima.
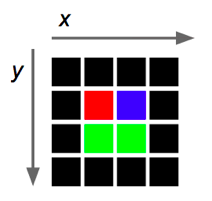
**Figura 1.** La imagen muestra la dirección en que se ordenan las coordenadas en las imágenes de `Qt`.
* Cuando queremos insertar datos bi-dimensionales (como las entradas de una cuadrilla que tiene coordenadas en $x$ y $y$) en un arreglo de una dimensión usamos una fórmula para convertir cada coordenada $(x,y)$ a un índice $i$ del arreglo. Para cada punto con coordenadas $(x,y)$ en la cuadrilla, evaluamos $i=(número-de-columnas)*y+x$, en donde `número-de-columnas` representa el ancho del arreglo bi-dimensional, y el resultado $i$ será el índice del arreglo de una dimensión que corresponde al punto con coordenadas $(x,y)$ en la cuadrilla. Por ejemplo, el índice $i$ correspondiente al punto $(1,2)$ en una cuadrilla de ancho $5$ es $i=(5)*2+1=11$.
---
---
## Bibliotecas
Para este proyecto necesitarás utilizar las funciones de `QtGlobal` para la implementación del círculo:
* `int qFloor(qreal v)` // Devuelve el "piso" del valor $v$.
* `qreal qSqrt(qreal v)` // Devuelve la raíz cuadrada del valor $v$.
* `qreal qPow(qreal x, qreal y)` // Devuelve el valor de $x$ elevado a la potencia $y$.
También necesitarás utilizar la función que pinta en la cuadrilla:
* `void switchOn(int x, int y, const QColor& color);` // Pinta la celda $(x,y)$ con el color dado. (No tienes que preocuparte por `QColor` porque se pasa a la función por parámetro.)
Aunque no se ve en el archivo `tools.cpp`, hay una arreglo llamado `mColors` que contiene el color de todas las celas de la cuadrilla. Esto te ayudará a saber cuál color está en una celda: `mColors[columns * y + x]`. Nota que el índice de este arreglo se calcula utilizando la conversión para cambiar coordenadas $(x,y)$ a índices que explicamos arriba.
---
---
!INCLUDE "../../eip-diagnostic/gridplot/es/diag-gridplot-01.html"
!INCLUDE "../../eip-diagnostic/gridplot/es/diag-gridplot-02.html"
---
---
## Sesión de laboratorio:
### Ejercicio 1: Implementar las funciones para hacer funcionar los botones de dibujar líneas
####Instrucciones
1. Descarga la carpeta `recursion-GridPlotter` de `Bitbucket` usando un terminal, moviéndote al directorio `Documents/eip`, y escribiendo el comando `git clone http://bitbucket.org/eip-uprrp/recursion-gridplotter`.
2. Carga a Qt creator el proyecto `GridPlotter` haciendo doble "click" en el archivo `GridPlotter.pro` que se encuentra en la carpeta `Documents/eip/recursion-gridplotter` de tu computadora.
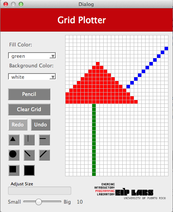
3. El proyecto contiene el esqueleto para una aplicación para dibujar líneas o figuras en una cuadrilla. La aplicación tiene una interface que le permite al usuario seleccionar el color para pintar, el color para el trasfondo de la cuadrilla, la figura que se va a dibujar (por ejemplo, círculo, cuadrado) y el tamaño de la figura. La figura seleccionada se dibuja cuando el usuario marca una celda en la cuadrilla.
Estarás trabajando en el archivo `tools.cpp`. Tu primera tarea es implementar las funciones `RowMajorFill`, `ColMajorFill`, `DiagonalLeft` y `DiagonalRight` que hacen que los botones para dibujar líneas funcionen. La función `RowMajorFill` ya está implementada para que la tengas de ejemplo. Las funciones deben trabajar como se indica adelante.
##### `RowMajorFill`
Cuando se selecciona la figura de línea horizontal en la interface, se dibujará una línea horizontal en la cuadrilla en la fila en donde el usuario marcó. La línea se expandirá a la derecha y a la izquierda de la celda marcada hasta que encuentre una celda (píxel) de un color diferente al color en el trasfondo, o hasta que la cuadrilla termine. La Figura 2 ilustra este comportamiento.
| (a) | (b) | (c) |
|---|----|----|
| 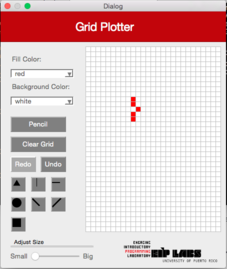 | 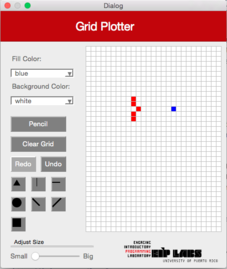 | 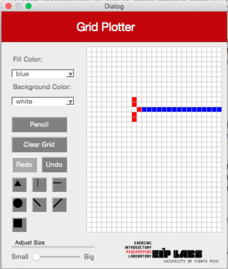|
**Figura 2** - (a) Un dibujo con trasfondo blanco y puntos rojos. (b) Cuando el usuario marca el botón de línea horizontal (`RowMajorFill`) y marca la celda mostrada, (c) se dibuja una línea horizontal que se expande hacia la izquierda y hacia la derecha de la celda marcada, hasta que se encuantra una celda con un color diferente al color de trasfondo.
##### `ColMajorFill`
Esta función debe trabajar de manera similar a la función `RowMajorFill` pero para columnas. La Figura 3 ilustra su comportamiento.
| (a) | (b) | (c) |
|---|----|----|
| 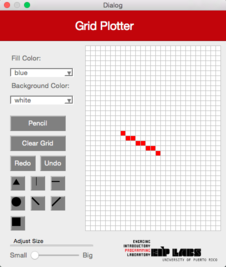 | 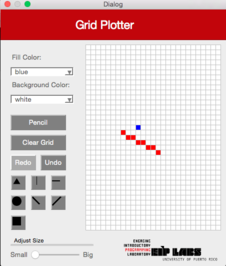 | 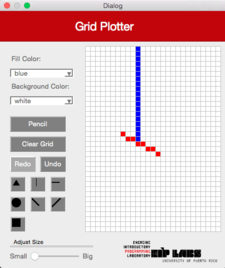|
**Figura 3** - (a) Un dibujo con trasfondo blanco y puntos rojos. (b) Cuando el usuario marca el botón de línea vertical (`ColMajorFill`) y marca la celda mostrada, (c) se dibuja una línea vertical que se expande hacia arriba y hacia abajo de la celda marcada, hasta que se encuantra una celda con un color diferente al color de trasfondo.
##### `DiagonalLeft`
Esta función debe trabajar de manera similar a la función `RowMajorFill` pero produce una línea diagonal desde la izquierda superior hasta la derecha inferior. La Figura 4 ilustra su comportamiento.
| (a) | (b) | (c) |
|---|----|----|
| 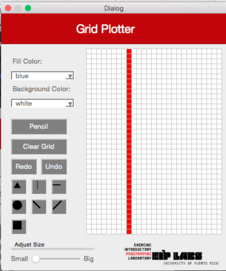 | 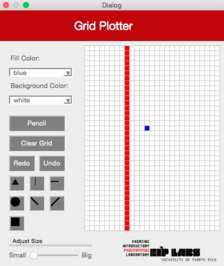 | 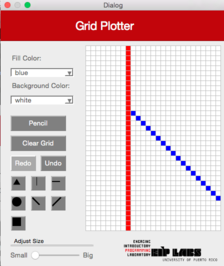|
**Figura 4** - (a) Un dibujo con trasfondo blanco y puntos rojos. (b) Cuando el usuario marca el botón de línea diagonal izquierda (`DiagonalLeft`) y marca la celda mostrada, (c) se dibuja una línea diagonal izquierda que se expande hacia arriba a la izquierda y hacia abajo a la derecha de la celda marcada, hasta que se encuantra una celda con un color diferente al color de trasfondo.
##### `DiagonalRight`
Esta función debe trabajar de manera similar a la función `DiagonalLeft` pero produce una línea diagonal desde la derecha superior hasta la izquierda inferior. La Figura 5 ilustra su comportamiento.
| (a) | (b) | (c) |
|---|----|----|
|  |  | 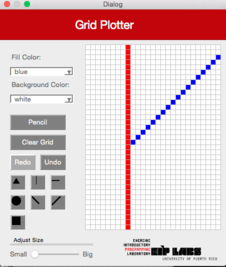|
**Figura 5** - (a) Un dibujo con trasfondo blanco y puntos rojos. (b) Cuando el usuario marca el botón de línea diagonal derecha (`DiagonalRight`) y marca la celda mostrada, (c) se dibuja una línea diagonal derecha que se expande hacia arriba a la derecha y hacia abajo a la izquierda de la celda marcada, hasta que se encuantra una celda con un color diferente al color de trasfondo.
### Ejercicio 2: Implementar las funciones para hacer funcionar los botones de dibujar cuadrados, triángulos y círculos.
Ahora implementarás la funcionalidad para dibujar cuadrados, círculos y líneas. El **tamaño** de la figura dibujada dependerá del tamaño seleccionado con la barra deslizante en la interface.
#### 2a: Cuadrados
Para los cuadrados, ¡lo más fácil es pensar en ellos como si fueran cebollas! Un cuadrado de tamaño 1 es simplemente la celda marcada por el usuario. Un cuadrado de tamaño 2 es la celda marcada, cubierta por una capa de celdas de tamaño 1, y así sucesivamente. En otras palabras, un cuadrado de tamaño $n$ tendrá alto = ancho = $2n-1$.
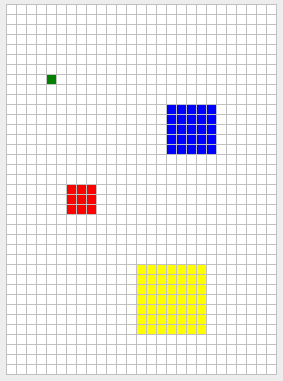
**Figura 6** - Cuadrados de tamaño 1 (verde), 2 (rojo), 3 (azul), y 4 (amarillo). En cada caso, el usuario marcó la celda del centro del cuadrado.
#### 2b: Triángulos
El botón de triángulo produce un triángulo **isóceles** como se muestra en la Figura 7. Para un tamaño $n$ seleccionado, el tamaño de la base será $2n + 1$. La altura debe ser $n+1$.

**Figura 7** - Triángulos de tamaño 1 (verde), 2 (rojo), 3 (azul), y 4 (amarillo). En cada caso, el usuario marcó la celda del centro de la base del triángulo.
#### 2c: Círculos
¡Felicitaciones! ¡Llegaste hasta la parte más difícil: círculos! Aquí tendrás que utilizar tus destrezas matemáticas ... esperamos que te haya ido bien en tu clase de pre-cálculo ...

**Figura 8** - Círculos de tamaño 1 (verde), 2 (rojo), 3 (azul), y 4 (amarillo). En cada caso, el usuario marcó la celda del centro del círculo.
**Ayuda para producir los círculos:**
Primero necesitas entender las expresiones asociadas a un círculo con ecuación: $x^2+y^2=r^2$. Por ejemplo, consideremos un círculo con radio $r=1$. La ecuación $x^2+y^2=1$ nos dice que todo punto $(x,y)$ que satisfaga la ecuación es un punto en la *circunferencia* del círculo. La expresión para un círculo *relleno* es: $x^2 + y^2 <=r^2$. Un círculo relleno, de radio $r=1$ tiene expresión $x^2 + y^2 <= 1$, lo que dice que cualquier punto $(x,y)$ que satisfaga $x^2 + y^2 <= 1$ es un punto en el círculo relleno.
¿Cómo producimos el círculo? Una manera sería generar todos los puntos **cercanos** al centro del círculo y determinar si éstos satisfacen la expresión $x^2 + y^2 <= r^2$. Por ejemplo, podemos tratar todos los puntos que están en el cuadrado de tamaño $2r+1$. Para un círculo de radio $r=2$ tendríamos que generar los siguientes puntos y probarlos en la expresión $x^2 + y^2 <=4$:
````
(-2, 2) (-1, 2) ( 0, 2) ( 1, 2) ( 2, 2)
(-2, 1) (-1, 1) ( 0, 1) ( 1, 1) ( 2, 1)
(-2, 0) (-1, 0) ( 0, 0) ( 1, 0) ( 2, 0)
(-2,-1) (-1,-1) ( 0,-1) ( 1,-1) ( 2,-1)
(-2,-2) (-1,-2) ( 0,-2) ( 1,-2) ( 2,-2)
````
En este caso, solo los puntos que se muestran abajo satisfacen la expresión $x^2 + y^2 <=4$.
````
( 0, 2)
(-1, 1) ( 0, 1) ( 1, 1)
(-2, 0) (-1, 0) ( 0, 0) ( 1, 0) ( 2, 0)
(-1,-1) ( 0,-1) ( 1,-1)
( 0,-2)
````
### Ejercicio 3: Implementar la función para rellenar figuras utilizando recursión.
En este ejercicio implementarás la funcionalidad para rellenar de color las figuras. Una de las maneras más convenientes para expresar el algoritmo para rellenar es utilizando recursión. Un algoritmo recursivo básico (pero bastante flojo) se encuentra en Wikipedia:
```
Relleno (celda, color-buscado, color-reemplazo):
1. Si color-buscado es igual al color-reemplazo, return.
2. Si el color de celda no es igual al color-buscado, return.
3. Ajusta el color de celda al color-reemplazo.
4. Ejecuta Relleno (un lugar a la izquerda de celda, color-buscado, color-reemplazo).
Ejecuta Relleno (un lugar a la derecha de celda, color-buscado, color-reemplazo).
Ejecuta Relleno (un lugar arriba de celda, color-buscado, color-reemplazo).
Ejecuta Relleno (un lugar abajo de celda, color-buscado, color-reemplazo).
5. Return.
```
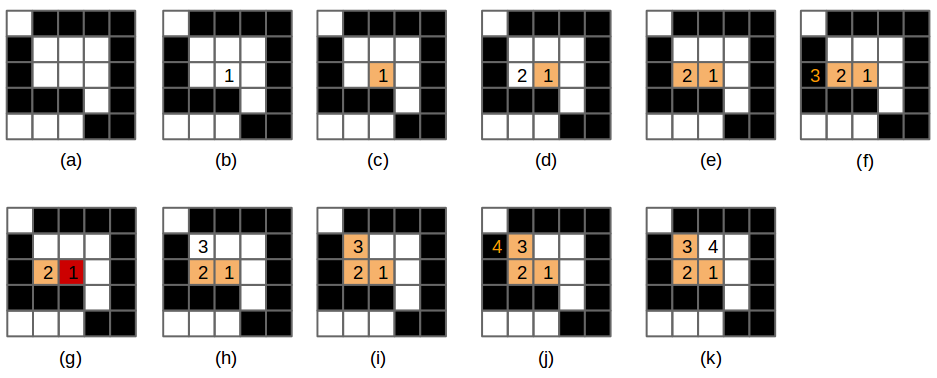
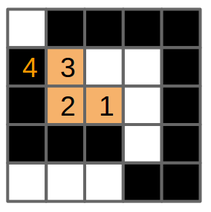
**Figura 9** - (a) El dibujo original con trasfondo blanco y celdas negras. (b) Se selecciona una celda y se ejecuta el algoritmo de rellenar en esa celda (1), (c) La celda se pinta anaranjada, entonces (d) invoca `relleno` en la celda de la izquierda (2). (e) La celda 2 se pinta anaranjada, entonces (f) invoca `relleno` en la celda de la izquierda (3). Esta celda no es de color-buscado (es negra), la función regresa (returns).
(g) `relleno` se invoca en la celda de la derecha de la celda 2, pero esa celda ya está pintada del color-reemplazo. (h) `relleno` se invoca en la celda de arriba de la celda 2. (i) Esta celda se pinta anaranjada e (j) invoca `relleno` en la celda de la izquierda (4). Esta celda no es de color-buscado, por lo tanto la función regresa (k), celda (3) invoca `relleno` en su celda derecha.
Invoca la función relleno (`flood-fill`) y prueba su funcionamiento utilizando varias figuras. Asegúrate de probar figuras abiertas, como, por ejemplo, la siguiente:
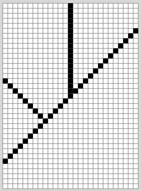
---
---
## Entregas
Utiliza "Entrega" en Moodle para entregar el archivo `tools.cpp` con las funciones que implementaste en esta experiencia de laboratorio. Recuerda utilizar buenas prácticas de programación, incluir el nombre de los programadores y documentar tu programa.
---
---
##Referencias
[1] Alyce Brady and Pamela Cutter, http://nifty.stanford.edu/2005/GridPlotter/
[2] Sacha Schutz, http://www.labsquare.org
[3] http://en.wikipedia.org/wiki/Flood_fill
---
---
---
---
----