recursion-gridplotter/README-en.md

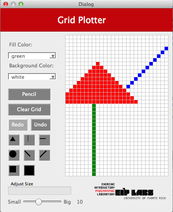
Recursion - Grid Plotter

[Verano 2016- Tatiana - Ive - Tatiana]

Recursion is a technique that is commonly used in programming. With this technique, problems are done by solving similar problems but for smaller cases. We can construct sets of objects or tasks using recursive rules and initial values. Recursive functions are functions that are self-invoking, using smaller sets or elements each time, until reaching a point where an initial value is used instead of self-invoking. In this laboratory experience, you will implement some tools to draw and practice the use of recursive functions to fill with color some figures.

Objectives:

1. Define and implement recursive functions.
2. Practice the use of repetition structures.

This laboratory experience is an adaptation of the task GridPlotter presented by Alyce Brady and Pamela Cutter in [1]. The implementation of the grid and the ability to paint in it was presented by Sacha Schutz in [2] but it was fixed, modified and adapted for this laboratory experience.

Pre-Lab:

Before arriving at the laboratory you should have:

1. Reviewed the concepts related to recursive functions.

2. Studied the concepts and instructions for the laboratory session.

3. Taken the Pre-Lab quiz, available in Moodle.

---

---

Drawing Applications

Probably many Windows OS users (if not all of them) have used the program called Paint, which is a simple drawing application. In that program, like many other drawing programs, there are several tools (for example: the pencil, the paint bucket and the line) that let the user draw on the area in different ways.

In this laboratory experience, we will make some tools (square, circle, triangle, some special lines) work … don’t worry!, we will do it in a very simple way.

The drawing will be on a grid. The tools will be used by clicking any cell in the grid and, from that point, the necessary cells that make the figure will be painted. For example, if we choose the vertical line tool and we click the cell in position (2,3), a vertical line will be drawn in all of the cells in column 2. That is, all of the cells in position $(2,y)$ will be marked for all of the $y$ in the grid.

---

---

Qt Coordinates

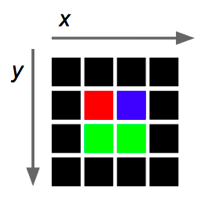
• The coordinate system in Qt works a bit differently, as it is shown in Figure 1. The entries go from left to right, from 0 to the maximum width, and from top to bottom, from 0 to the maximum height.

  

  Figure 1. The image shows the direction in which the coordinates are ordered in Qt images.

• When we want to insert two-dimensional data (like the entries of a grid that has coordinates in $x$ and $y$) in an one-dimensional array we use a formula to convert every coordinate $(x,y)$ to an index $i$ of the array. For every point with coordinates $(x,y)$ in the grid, we evaluate $i=(number-of-columns)*y+x$, where number-of-columns represents the width of the two-dimensional array, and the result $i$ will be the index of the one-dimensional array that corresponds to the point with coordinates $(x,y)$ in the grid. For example, the index $i$ that corresponds to the point $(1,2)$ in the grid of width $5$ is $i=(5)*2+1=11$.

---

---

Libraries

In this project, you will need to use the following QtGlobal functions for the implementation of the circle.

• int qFloor(qreal v) // Returns the “floor” value $v$.
• qreal qSqrt(qreal v) // Returns the square root of the value $v$.
• qreal qPow(qreal x, qreal y) // Returns the value of $x$ to the power of $y$.

In addition, you will need to use the function that paints the grid:

• void switchOn(int x, int y, const QColor& color); // Paints the cell $(x,y)$ with the given color. (You don’t have to worry about QColor because it is passed by the function’s parameter)

Although the archive tools.cpp is not visible, there is an array called mColorsthat contains the color of all the cells in the grid. This will help you know which color is in the cell: mColors[columns * y + x]. Note that the index of the array is calculated using the conversion explained above that changes the coordinates $(x,y)$ to an index.

---

---

!INCLUDE “../../eip-diagnostic/gridplot/es/diag-gridplot-01.html”

!INCLUDE “../../eip-diagnostic/gridplot/es/diag-gridplot-02.html”

---

---

Laboratory Session:

Exercise 1 - Implement the Functions that Operate the Buttons for Drawing Lines

Instructions

1. Load the project GridPlotter into QtCreator. There are two ways to do this:

   • Using the virtual machine: Double click the file GridPlotter.pro located in the folder home/eip/labs/recursion-gridplotter of your virtual machine.
   • Downloading the project’s folder from Bitbucket: Use a terminal and write the command git clone http://bitbucket.org/eip-uprrp/recursion-gridplotter to download the folder recursion-gridplotter from Bitbucket. Double click the file GridPlotter.pro located in the folder that you downloaded to your computer.
     

2. The project contains the skeleton for the application that draws lines and figures in a grid. The application has an interface that allows the user to select the color we want to draw with, the color of the background of the grid, the figure you want to draw (for example, circle or square) and the size of the figure. The selected figure is drawn when the user clicks a cell in the grid.

You will be working with the archive called tools.cpp. Your first task is to implement the functions RowMajorFill, ColMajorFill, DiagonalLeft and DiagonalRight that make the buttons that draw lines work. The function RowMajorFill is already implemented for you to use as an example. The functions should work as indicated below.

RowMajorFill

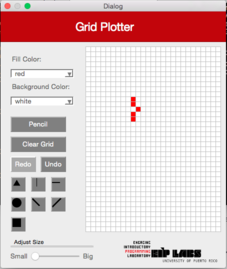
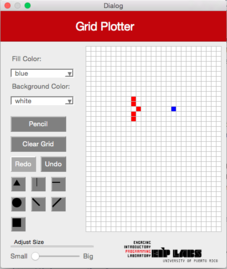
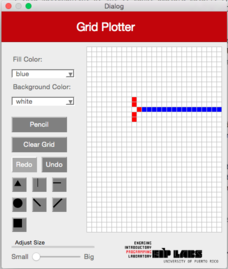
When you select the horizontal line figure in the interface, a horizontal line will be drawn on the row of the grid the user clicked. The line will expand to the right and left of the clicked cell until it finds a cell (pixel) with a different color as the background color, or until the grid ends. Figure 2 illustrates this behavior.

| (a) | (b) | © |
|---|----|----| | | | |

Figure 2. (a) A drawing with a white background with red dots. (b) When the user clicks on the horizontal line button (RowMajorFill) and clicks the cell shown, © a horizontal line that expands to the left and to the right of the cell clicked is drawn, until it finds a cell with a different color from the color of the background.

ColMajorFill

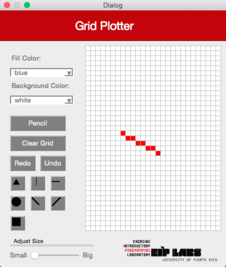
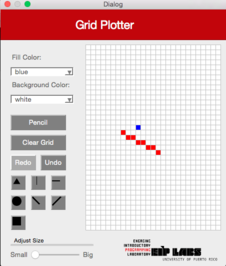
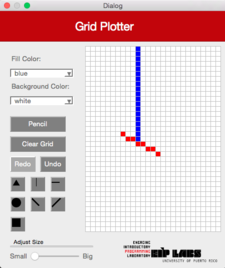
This function should work similarly as the function RowMajorFill but for columns. Figure 3 illustrates its behavior.

| (a) | (b) | © | |---|----|----| | | | |

Figure 3. (a) A drawing with a white background and red dots (b) When the user clicks on the vertical line button (ColMajorFill) and clicks the cell shown, © a vertical line that expands to the left and to the right of the cell clicked is drawn, until it finds a cell with a different color from the color of the background.

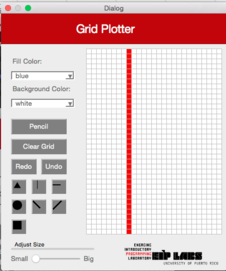
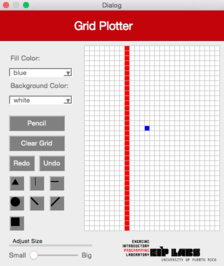
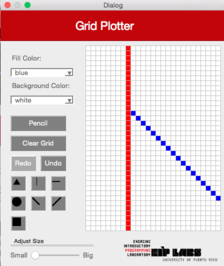
DiagonalLeft

This function should work similarly as the RowMajorFill function but produces a diagonal line from the left superior corner to the right inferior corner. Figure 4 illustrates its behavior.

| (a) | (b) | © | |---|----|----| | | | |

Figure 4. (a) A drawing with a white background and red dots. (b) When the user clicks on the left diagonal line button (DiagonalLeft) and clicks the cell shown, © a left diagonal line that expands towards the top to the left and towards the bottom to the right of the cell clicked is drawn, until it finds a cell with a different color from the color of the background.

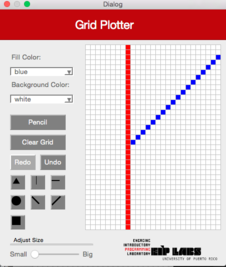
DiagonalRight

This function should work similarly as the DiagonalLeft function but produces a diagonal line from the superior right corner to the inferior left corner. Figure 5 illustrates its behavior.

| (a) | (b) | © | |---|----|----| | | | |

Figure 5. (a) A drawing with a white background and red dots. (b) When the user clicks on the right diagonal line button (DiagonalRight) and clicks the cell shown, © a right diagonal line that expands towards the top to the right and towards the bottom to the left of the cell clicked is drawn, until it finds a cell with a different color from the color of the background.

Exercise 2 - Implement the Functions that Operate the Buttons for Drawing Squares, Triangles and Circles.

Now, you will implement the functionality to draw squares, circles and triangles. The size of the figure drawn will depend on the size selected on sliding bar in the interface.

2a: Squares

For the squares, the easiest way to think of it is as if they were onions! A square of size 1 is simply the cell clicked by the user. A square of size 2 is the cell clicked by the user, covered by a layer of cells of size 1, and so on. In other words, a square of size $n$ will have height = width = $2n-1$.

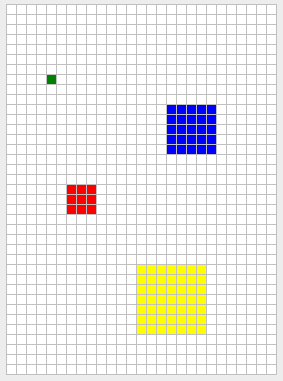
Figure 6. Squares of size 1 (green), 2 (red), 3 (blue), and 4 (yellow). In each case, the user clicked the center of the square.

2b: Triangles

The triangle button produces an isosceles triangle as it is shown in Figure 7. For a selected size $n$, the size of the base will be $2n + 1$. The height should be $n+1$.

Figure 7. Triangles of size 1 (green), 2 (red), 3 (blue), and 4 (yellow). In each case, the user clicked the center of the base of the triangle.

2c: Circles

Congratulations! You got to the most difficult part: circles! Here you’ll need to use your mathematical skills… we hope that you did well on your pre-calculus class…

Figure 8. Circles of size 1 (green), 2 (red), 3 (blue), and 4 (yellow). In each case, the user clicked the center of the circle.

Help Producing Circles:

First of all, you need to understand that the terms associated with a circle that has an equation: $x^2+y^2=r^2$. For example, consider a circle with radius $r=1$. The equation $x^2+y^2=1$ tells us that every point $(x,y)$ that satisfies the equation is a point in the circle’s circumference. The expression for a filled circle is : $x^2 + y^2 <=r^2$. A filled circle, of radius $r=1$ has the expression $x^2 + y^2 <= 1$, which says that every point $(x,y)$ that satisfies $x^2 + y^2 <= 1$ is a point in a filled circle.

How do we produce a circle? One way would be to generate all the points near the center of the circle and determine if those satisfy the expression $x^2 + y^2 <= r^2$. For example, we can try all of the points that are in the square of size $2r+1$. For the circle of radius $r=2$ we would have to generate the following points and prove them in the expression $x^2 + y^2 <=4$:

(-2, 2) (-1, 2) ( 0, 2) ( 1, 2) ( 2, 2)
(-2, 1) (-1, 1) ( 0, 1) ( 1, 1) ( 2, 1)
(-2, 0) (-1, 0) ( 0, 0) ( 1, 0) ( 2, 0)
(-2,-1) (-1,-1) ( 0,-1) ( 1,-1) ( 2,-1)
(-2,-2) (-1,-2) ( 0,-2) ( 1,-2) ( 2,-2)

In this case, only the points that are shown below satisfy the expression $x^2 + y^2 <=4$.

                ( 0, 2) 
        (-1, 1) ( 0, 1) ( 1, 1) 
(-2, 0) (-1, 0) ( 0, 0) ( 1, 0) ( 2, 0)
        (-1,-1) ( 0,-1) ( 1,-1) 
                ( 0,-2) 

Exercise 3 - Implement the Function that Fills the Figures using Recursion.

In this exercise you will implement the functionality to fill the color of the figures.One of the more convinient ways to express the algorithm to fill the figures is using recursion. A basic recursive algorithm (but it’s pretty weak) is found in Wikipedia:

Flood Fill (cells, target-color, replacement-color):
 1. If target-color is the same to replacement-color, return.
 2. If the color of the cell is not the same as target-color, return. 
 3. Adjust the color of the cell to replacement-color.
 4. Execute Flood Fill (one step to the left of the cell, target-color, replacement-color).
    Execute Flood Fill (one step to the right of the cell, target-color, replacement-color).    Execute Flood Fill (one step to the top of the cell, target-color, replacement-color).
    Execute Flood Fill (one step to the bottom of the cell, target-color, replacement-color).
 5. Return.

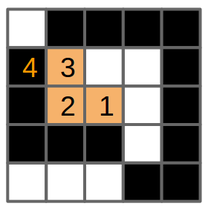
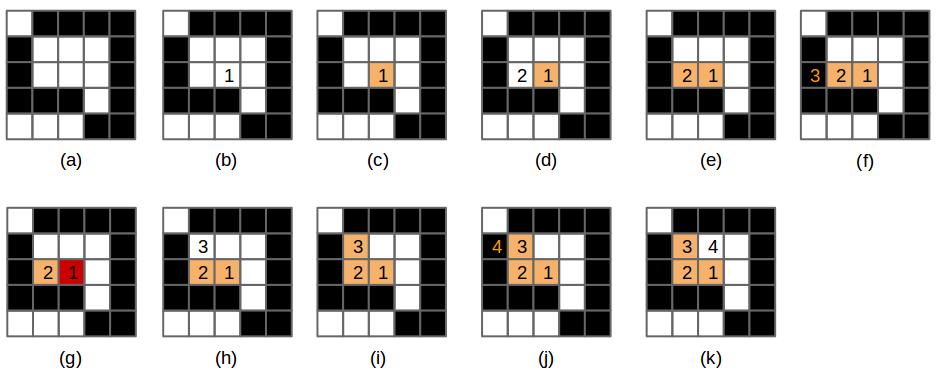
Figure 9. (a) The original drawing with a white background and black cells. (b) A cell is selected and the algorithm is executed to fill the cell (1), © The cell is painted orange, then (d) invokes flood-fill on the left cell (2). (e) The cell 2 is painted orange, then (f) invokes flood-fill on the cell of the left (3). This cell is not the target-color (its black), and the function returns. (g) flood-fill is invoked on the cell on the right of cell 2, but that cell is already painted with the replacement-color. (h) flood-fill is invoked on the cell on top of the cell 2. (i) This cell is painted orange and (j) invokes flood-fill on the left cell (4). This cell is not the target-color, therefore the function returns (k), cell (3) invokes flood-fill on its right cell.

The function flood-fill is invoked and proves its functionality using various figures. You should assure that you proved open figures, for example, the following:

---

---

Deliverables

Use “Deliverable” in Moodle to hand in the archive tools.cpp with the functions that you implemented in this laboratory experience. Remember to use good programming techniques, include the names of the programmers involved, and document your program.

---

---

References

[1] Alyce Brady and Pamela Cutter, http://nifty.stanford.edu/2005/GridPlotter/

[2] Sacha Schutz, http://www.labsquare.org

[3] http://en.wikipedia.org/wiki/Flood_fill

---

---

---

---

---