# Recursion - Recursive Shapes



One commonly used programming technique is *recursion*. With this technique, problems are solved by solving similar problems, but for smaller cases. We can build sets of objects or tasks using *recursive rules* and *initial values*. *Recursive functions* are functions that are self-invoking, using smaller sets or elements each time, until reaching a point where the initial value is used instead of self-invoking. Fractals are an example of figures that can be created using recursion. In this laboratory experience, you will practice the definition and implementation of recursive functions to draw self-similar objects (fractals).
The exercises in this laboratory experience are an adaptation of https://sites.google.com/a/wellesley.edu/wellesley-cs118-spring13/lectures-labs/lab-6-turtle-recursion.
## Objectives:
1. Practice the definition and implementation of recursive functions.
## Pre-Lab:
Before coming to the laboratory session you should have:
1. Reviewed the basic concepts related to recursive functions.
2. Studied the `box` function to draw boxes, included in the `boxes.cpp` file in the `Qt` project.
3. Studied the concepts and instructions related to the laboratory session.
4. Taken the Pre-Lab quiz, available in Moodle.
---
---
## Self-similar Forms

**Figure 2.** Fractal tree [5].
---
One ingenious way of practicing and visualizing recursion is programming functions that produce recursive figures, or fractals. For example, consider a recursive figure that we'll call *branch*. Figure 3 shows `branch(0,90)`, `branch(1,90)`, and `branch(2,90)`.
---
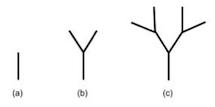
**Figure 3.** (a) `branch(0,90)`, (b) `branch(1,90)`, y (c) `branch(2,90)`.
---
Can you see the recursive behavior in this figure? Notice that `branch(0,90)` is only a vertical segment (a segment in an angle of 90 degrees); `branch(1,90)` is `branch(0,90)` with two segments inclined in its top. More precisely, `branch(1,90)` is `branch(0,90)` with a `branch(0,60)` and a `branch(0,120)` in its top. Similarly, `branch(2,90)` is `branch(0,90)` with two `branch(1,90)` inclined in the top. That is, `branch(2,90)` is:
`branch(0,90)` with a `branch(1,60)` and a `branch(1,120)` in its top. Notice that $$60=90-30$$ and $$120=90+30$$.
This way we can express `branch(n,A)` as a composition of branches with $$n$$ smaller and inclined branches. Code 1 provides a way of expressing `branch` as a recursive function.
---
```
branch(0, A) = draws a segment of length L and angle A
branch(n, A) = draws: branch(0,A), branch(n-1,A-30), branch(n-1,A+30)
```
**Code 1.** Function to draw branches.
---
Notice that the recursive definition includes a base case, that is, includes `branch(0,A)`, and a recurrence relation, that is, `branch(n,A)`. To simplify, we assume that `branch(n-1,A-30)` and `branch(n-1,A+30)` are drawn at the top of `branch(0,A)`.
Figure 4 illustrates the recursive expansion for `branch(2,90)`. The color of each expression is the corresponding segment color in the figure.
---
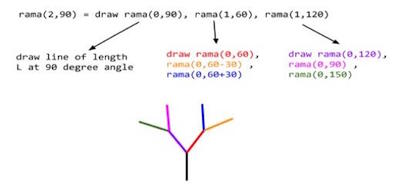
**Figure 4.** Illustration for `branch(2,90)`.
---
Can you predict how the next iteration for the figure will look? That is, what figure will `branch(3,A)` produce?
---
---
!INCLUDE "../../eip-diagnostic/recursive-shapes/en/diag-recursive-shapes-01.html"
!INCLUDE "../../eip-diagnostic/recursive-shapes/en/diag-recursive-shapes-02.html"
---
---
## Laboratory Session:
In today's laboratory experience you will implement recursive functions to produce fractals.
### Exercise 1 - Snowflake
One of the simplest fractal figures is the snowflake. This figure is formed by an isosceles triangle, substituting the middle third segment on each side by an inverted "V". The measurements of each side of the "V" is equal to the measurements of the segment it substitutes. We will use the snowflake to illustrate the process of recursion.
---
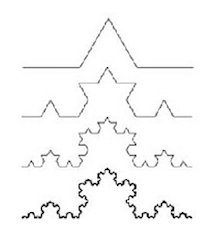
**Figure 5.** Part of the construction of the snowflake fractal.
---
#### Instructions
1. Load the project `RecursiveShapes` into `QtCreator`. There are two ways to do this:
* Using the virtual machine: Double click the file `RecursiveShapes.pro` located in the folder `/home/eip/labs/recursion-recursiveshapes` of your virtual machine.
* Downloading the project’s folder from `Bitbucket`: Use a terminal and write the command `git clone http:/bitbucket.org/eip-uprrp/recursion-recursiveshapes` to download the folder `recursion-recursiveshapes` from `Bitbucket`. Double click the file `RecursiveShapes.pro` located in the folder that you downloaded to your computer.
2. Compile and run the program so you see a snowflake figure constructed with 3 iterations of the `snowflake` function. You can see the code of this function in the `snowflake.cpp` file of the `Qt` project.
In the `main` function, look up the line where the variable `level` is declared and given a value. Change the value of `level` to `0` and run the program. You'll be able to see the triangle that represents the recursive base case for the snowflake. Continue changing the value for `level` and running the program so you can see the recursion process and produce self-similar figures.
### Exercise 2 - Self-similar Boxes
In this exercise, your task is to program a recursive function `boxes`, in the file `boxes.cpp`, that produces the following figures.
---
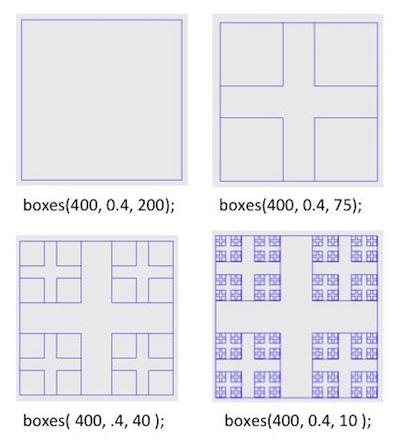
**Figure 6.** Illustration of the box figures that your program should produce.
---
The `boxes` recursive function includes three parameters: `sideLength`, `shrinkFactor`, and `smallestLength`.
* `sideLength`: an integer that determines the length of the sides of the largest box.
* `shrinkFactor`: a real number that determines the rate of the next level of boxes. For example, if `sideLength` is `100`, and `shrinkFactor` is `0.3`, the length of the sides of the largest box will be `100` units, and the length of the sides of the smallest box will be `100*.3=30` units. Four copies of that smaller box are placed within the previous box, **one box in each corner**.
* `smallestLength`: is an integer that determines the length of the sides of the smallest box that will be drawn. For example, in Figure 6, `boxes(400,0.4,200)` only draws the box with sides of length `400`, since the size that will follow will be `400 * 0.4 = 160`, which is smaller than `200`. On the other hand, `boxes(400, 0.4, 75)` draws the box of size `400` and the boxes with size `160`, but not the following ones in size, since they would be of size `160 * 0.4 = 64`, which is less than `75`.
#### Instructions
1. Study the `box` function included in the `boxes.cpp` file. This function receives as arguments the coordinates of the upper left corner, the length of the sides and the color of the box. The function draws a box with these specifications.
2. Write a recursive algorithm for the `boxes` function described above. Remember to include the base case! The algorithm should also invoke the `box` function to draw the boxes.
3. Implement the function in `QtCreator`. You will need to provide additional parameters to your function so you can control the position and the color of the squares.
4. Invoke the `boxes` function from the `main` function in the `main.cpp` file. Compare your results with the images in Figure 6.
---
---
## Deliverables
1. Use "Deliverables" in Moodle to upload the `boxes.cpp` and `main.cpp` files. Remember to use good programming techniques, include the names of the programmers involved, and document your program.
---
---
## References
[1] https://sites.google.com/a/wellesley.edu/wellesley-cs118-spring13/lectures-labs/lab-6-turtle-recursion.
[2] "Mandel zoom 00 mandelbrot set". Licensed under Creative Commons Attribution-Share Alike 3.0 via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Mandel_zoom_00_mandelbrot_set.jpg#mediaviewer/File:Mandel_zoom_00_mandelbrot_set.jpg
[3] "Mandel zoom 04 seehorse tail". Licensed under Creative Commons Attribution-Share Alike 3.0 via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Mandel_zoom_04_seehorse_tail.jpg#mediaviewer/File:Mandel_zoom_04_seehorse_tail.jpg
[4] http://www.coolmath.com/fractals/images/fractal5.gif
[5] "Fractal tree (Plate b - 2)". Licensed under Public domain via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Fractal_tree_(Plate_b_-_2).jpg#mediaviewer/File:Fractal_tree_(Plate_b_-_2).jpg