EIP
/
recursion-recursiveshapes
İzle 2
Yıldızla 0
Çatalla 0
Kod Sorunlar 0 Değişiklik İstekleri 0 Sürümler 0 Wiki Aktivite
Açıklama Yok
12 İşlemeler
1 Dal
Ağaç: 1d53368a4a
Dallar Biçim İmleri
${ item.name }
Branş ${ searchTerm } oluştur
'1d53368a4a'den
${ noResults }
recursion-recursiveshapes/README-es.md

README-es.md 9.0KB
Geçmiş Ham

Recursión - Figuras Recursivas

main1.jpg main2.jpg main3.png

[Verano 2016 - Ive - Coralys]

Una técnica muy utilizada en programación es la recursión. Con esta técnica se resuelven problemas resolviendo un problema similar, pero para casos más pequeños. Podemos construir conjuntos de objetos o procesos utilizando reglas recursivas y valores iniciales. Las funciones recursivas son funciones que se auto-invocan, utilizando cada vez conjuntos o elementos más pequeños, hasta llegar a un punto en donde se utiliza el valor inicial en lugar de auto-invocarse. Los fractales son un ejemplo de figuras que se pueden crear usando recursión. En esta experiencia de laboratorio practicarás la definición e implementación de funciones recursivas para dibujar formas auto-similares (fractales).

Los ejercicios de esta experiencia de laboratorio son una adaptación de https://sites.google.com/a/wellesley.edu/wellesley-cs118-spring13/lectures-labs/lab-6-turtle-recursion.

Objetivos:

  1. Practicar el definir e implementar funciones recursivas.

Pre-Lab:

Antes de llegar al laboratorio debes haber:

  1. Repasado los conceptos relacionados a funciones recursivas.

  2. Estudiado la función box para dibujar cajas, incluida en el archivo boxes.cpp del proyecto de Qt.

  3. Haber estudiado los conceptos e instrucciones para la sesión de laboratorio.

  4. Haber tomado el quiz Pre-Lab disponible en Moodle.

Figuras auto-similares

figure2.png

Figura 2. Árbol fractal [5].

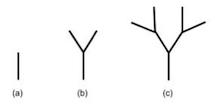
Una manera ingeniosa de practicar y visualizar recursión es programando funciones que produzcan figuras auto-similares (o recursivas). Por ejemplo, considera una figura recursiva que llamaremos rama. La Figura 3 muestra rama(0,90), rama(1,90) y rama(2,90).

figure3.jpg

Figura 3. (a) rama(0,90), (b) rama(1,90), y © rama(2,90).

¿Puedes ver el comportamiento recursivo de esta figura? Nota que rama(0,90) es solo un segmento vertical (un segmento en un ángulo de 90 grados); rama(1,90) es rama(0,90) con dos segmentos inclinados en su extremo superior. Más preciso, rama(1,90) es rama(0,90) con una rama(0,60) y una rama(0,120) en el extremo superior. Similarmente, rama(2,90) es rama(0,90) con dos rama(1,90) inclinadas en el extremo superior. Esto es, rama(2,90) es:

rama(0,90) con una rama(1,60) y una rama(1,120) en el extremo superior. Nota que $$60=90-30$$ y que $$120=90+30$$.

De esta manera podemos expresar rama(n,A) como una composición de ramas de $$n$$ ramas más pequeñas e inclinadas. El Código 1 provee una manera de expresar rama como una función recursiva.

rama(0, A) = dibuja un segmento de largo L en un ángulo A
rama(n, A) = dibuja: rama(0,A), rama(n-1, A-30), rama(n-1, A+30)

Código 1. Función para dibujar las ramas.

Nota que la definición recursiva incluye un caso base, esto es, incluye rama(0,A), y una relación de recurrencia (o caso recursivo), esto es, rama(n,A). Para simplificar, asumimos que rama(n-1,A-30) y rama(n-1,A+30) se dibujan en el extremo superior de rama(0,A).

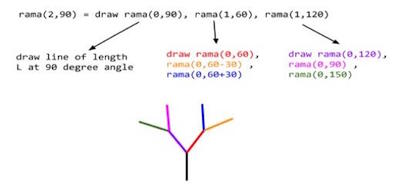
La Figura 4 ilustra la expansión recursiva para rama(2,90). El color de cada expresión es el color del segmento que le corresponde en la figura.

figure4.jpg

Figura 4. Ilustración de rama(2,90).

¿Puedes predecir cómo será la próxima iteración de la figura? Es decir, ¿qué figura producirá rama(3,A)?

!INCLUDE “../../eip-diagnostic/recursive-shapes/es/diag-recursive-shapes-01.html”

!INCLUDE “../../eip-diagnostic/recursive-shapes/es/diag-recursive-shapes-02.html”

Sesión de laboratorio:

En la experiencia de laboratorio de hoy implementarás funciones recursivas para producir fractales.

Ejercicio 1 - Copo de nieve

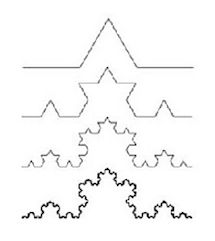
Una de las figuras fractales más simples es la figura de un copo de nieve. Esta figura se forma a partir de un triángulo isósceles, sustituyendo el segmento del tercio del medio de cada lado por una “V” invertida. La medida de los lados de la “V” es igual a la medida del segmento que sustituye. Usaremos el copo de nieve para ilustrar el proceso de recursión.

figure5.png

Figura 5. Parte de la construcción del fractal “copo de nieve”.

Instrucciones

  1. Carga a QtCreator el proyecto RecursiveShapes. Hay dos maneras de hacer esto:

    • Utilizando la máquina virtual: Haz doble “click” en el archivo RecursiveShapes.pro que se encuentra en el directorio /home/eip/labs/recursion-recursiveshapes de la máquina virtual.
    • Descargando la carpeta del proyecto de Bitbucket: Utiliza un terminal y escribe el comando git clone http:/bitbucket.org/eip-uprrp/recursion-recursiveshapes para descargar la carpeta recursion-recursiveshapes de Bitbucket. En esa carpeta, haz doble “click” en el archivo RecursiveShapes.pro.

  2. Compila y corre el programa para que veas una figura del copo de nieve construida con 3 iteraciones de la función snowflake. Puedes ver el código que define esta función en el archivo snowflake.cpp del proyecto de Qt.

En la función main, busca la línea en donde se declara y da valor a la variable level. Cambia el valor de level a 0 y corre el programa de nuevo. Podrás ver el triángulo que representa el caso base de la recursión para el copo de nieve. Continúa cambiando el valor de la variable level y corriendo el programa para que veas el proceso de la recursión y de producir figuras auto-similares.

Ejercicio 2 - Cajas autosimilares

Tu tarea en este ejercicio es programar una función recursiva boxes, en el archivo boxes.cpp, que produzca las siguientes figuras.

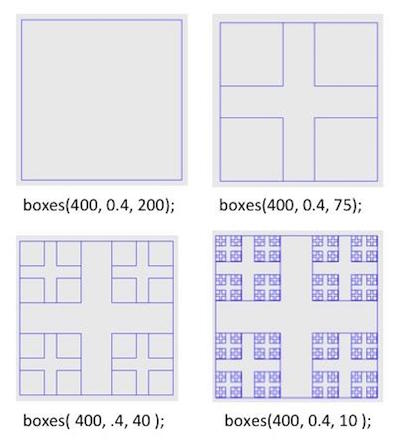
figure6.jpg

Figura 6. Ilustración de las figuras de cajas que debe producir tu programa.

La función recursiva boxes incluye tres parámetros: sideLength, shrinkFactor, y smallestLength.

  • sideLength: un entero que determina el largo de los lados del cuadrado más grande.
  • shrinkFactor: un número real que determina la razón del siguiente nivel de cuadrados. Por ejemplo, si sideLength es 100, y shrinkFactor es 0.3, el largo de los lados del cuadrado más grande será 100 unidades, y el largo de los lados del próximo cuadrado más pequeño será 100*.3=30 unidades. Se colocan 4 copias de ese cuadrado más pequeño dentro del cuadrado anterior, un cuadrado en cada esquina.
  • smallestLength: es un valor entero que determina el largo del lado del cuadrado más pequeño que será dibujado. Por ejemplo, en la Figura 6, boxes(400, 0.4, 200) solo dibuja el cuadrado con lados de largo 400, ya que el tamaño que le seguiría sería 400 * 0.4 = 160, que es más pequeño que 200. Por otro lado, boxes(400, 0.4, 75) dibuja el cuadrado de tamaño 400 y los cuadrados de tamaño 160, pero no los siguientes en tamaño, porque serían de tamaño 160 * 0.4 = 64, que es menor que 75.

Instrucciones

  1. Estudia la función box incluida en el archivo boxes.cpp. Esta función recibe como argumentos las coordenadas de la esquina superior izquierda, el largo de los lados y el color de una caja. La función dibuja una caja con esas especificaciones.

  2. Escribe un algoritmo recursivo para la función boxes descrita arriba. ¡Recuerda incluir el caso base! El algoritmo también debe invocar la función box para dibujar las cajas.

  3. Implementa la función en QtCreator. Necesitarás proveer parámetros adicionales a tu función para que puedas controlar la posición y el color de los cuadrados.

  4. Invoca la función boxes desde la función main en el archivo main.cpp. Compara tus resultados con las imágenes de la Figura 6.

Entrega

Utiliza “Entrega” en Moodle para entregar los archivos boxes.cpp y main.cpp. Recuerda utilizar buenas prácticas de programación, incluye el nombre de los programadores, y documenta tu programa.

Referencias

[1] https://sites.google.com/a/wellesley.edu/wellesley-cs118-spring13/lectures-labs/lab-6-turtle-recursion.

[2] “Mandel zoom 00 mandelbrot set”. Licensed under Creative Commons Attribution-Share Alike 3.0 via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Mandel_zoom_00_mandelbrot_set.jpg#mediaviewer/File:Mandel_zoom_00_mandelbrot_set.jpg

[3] “Mandel zoom 04 seehorse tail”. Licensed under Creative Commons Attribution-Share Alike 3.0 via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Mandel_zoom_04_seehorse_tail.jpg#mediaviewer/File:Mandel_zoom_04_seehorse_tail.jpg

[4] http://www.coolmath.com/fractals/images/fractal5.gif

[5] “Fractal tree (Plate b - 2)”. Licensed under Public domain via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Fractaltree(Plateb-_2).jpg#mediaviewer/File:Fractaltree(Plateb-_2).jpg