recursion-recursiveshapes/README-en.md

Recursion - Recursive Shapes

[Verano 2016 - Ive]

One commonly used programming technique is recursion. With this technique, problems are solved by solving similar problems but for smaller cases. We can construct sets of objects or tasks using recursive rules and initial values. Recursive functions are functions that are self-invoking, using smaller sets or elements each time, until reaching a point where an initial value is used instead of self-invoking. Fractals are an example of figures that can be created using recursion. In this laboratory experience you will practice the definition and implementation of recursive functions to draw self-similar objects (fractals).

The exercises in this laboratory experience are an adaptation of https://sites.google.com/a/wellesley.edu/wellesley-cs118-spring13/lectures-labs/lab-6-turtle-recursion.

Objectives:

1. Practice the definition and implementation of recursive functions.

Pre-Lab:

Before coming to the laboratory session you should have:

1. Reviewed the basic concepts related to recursive functions.

2. Studied the box function to draw boxes, included in the boxes.cpp file in the Qt project.

3. Studied the concepts and instructions related to the laboratory session.

4. Taken the Pre-Lab quiz available in Moodle.

---

---

Self-similar forms

Figure 2. Fractal tree [5].

---

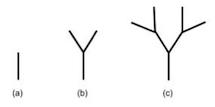
One ingenious way of practicing and visualize recursion is programming functions that produce recursive figures, or fractals. For example, consider a recursive figure that we’ll call branch. Figure 3 shows branch(0,90), branch(1,90), and branch(2,90).

---

Figure 3. (a) branch(0,90), (b) branch(1,90), y © branch(2,90).

---

Can you see the recursive behavior in this figure? Notice that branch(0,90) is only a vertical segment (a segment in an angle of 90 degrees); branch(1,90) is branch(0,90) with two segments inclined in its top. More precisely, branch(1,90) is branch(0,90) with a branch(0,60) and a branch(0,120) in its top. Similarly, branch(2,90) is branch(0,90) with two branch(1,90) inclined in the top. That is, branch(2,90) is: branch(0,90) with a branch(1,60) and a branch(1,120) in its top. Notice that $$60=90-30$$ and $$120=90+30$$.

This way we can express branch(n,A) as a composition of branches with smaller inclined $$n$$’s. Code 1 provides a way of expressing branch as a recursive function.

---

branch(0, A) = draws a segment of length L and angle A
branch(n, A) = draws: branch(0,A), branch(n-1,A-30), branch(n-1,A+30)

Code 1. Function to draw branches.

---

Notice that the recursive definition includes a base case, that is, includes branch(0,A), and a recurrence relation, that is, branch(n,A). To simplify, we assume that branch(n-1,A-30) and branch(n-1,A+30) are drawn at the top of branch(0,A).

Figure 4 illustrates the recursive expansion for branch(2,90). The color of each expression is the corresponding segment color in the figure.

---

Figure 4. Illustration for branch(2,90).

---

Can you predict how the next iteration for the figure will look? That is, what figure will branch(3,A) produce?

---

---

Laboratory Session

In today’s laboratory experience you will implement recursive functions to produce fractals.

Exercise 1 - Snowflake

One of the simplest fractal figures is the snowflake. This figure is formed by an isosceles triangle, substituting the middle third segment on each side by an inverted “V”. The measurements of each side of the “V” is equal to the measurements of the segment it substitutes. We will use the snowflake to illustrate the process of recursion.

---

Figure 5. Part of the construction of the snowflake fractal.

---

Instructions:

1. Load the project RecursiveShapes into QtCreator. There are two ways to do this:

   • Using the virtual machine: Double click the file RecursiveShapes.pro located in the folder /home/eip/labs/recursion-recursiveshapes of your virtual machine.
   • Downloading the project’s folder from Bitbucket: Use a terminal and write the command git clone http:/bitbucket.org/eip-uprrp/recursion-recursiveshapes to download the folder recursion-recursiveshapes from Bitbucket. Double click the file RecursiveShapes.pro located in the folder that you downloaded to your computer.

2. Compile and run the program so you see a snowflake figure constructed with 3 iterations of the snowflake function. You can see the code of this function in the snowflake.cpp file of the Qt project.

In the main function, look up the line where the variable level is declared and given a value. Change the value of level to 0 and run the program. You’ll be able to see the triangle that represents the recursive base case for the snowflake. Continue changing the value for level and running the program so you can see the recursion process and produce self-similar figures.

Exercise 2 - Self-similar boxes

In this exercise, your task is to program a recursive function boxes, in the file boxes.cpp, that produces the following figures.

---

Figure 6. Illustration of the box figures that your program should produce.

---

The boxes recursive function includes three parameters: sideLength, shrinkFactor, and smallestLength.

• sideLength: an integer that determines the length of the sides of the largest box.
• shrinkFactor: a real number that determines the rate of the next level of boxes. For example, if sideLength is 100, and shrinkFactor is 0.3, the length of the sides of the largest box will be 100 units, and the length of the sides of the smallest box will be 100*.3=30 units. Four copies of that smaller box are placed within the previous box, one box in each corner.
• smallestLength: is an integer that determines the length of the sides of the smallest box that will be drawn. For example, in Figure 6, boxes(400,0.4,200) only draws the box with sides of length 400, since the size that will follow will be 400 * 0.4 = 160, which is smaller than 200. On the other hand, boxes(400, 0.4, 75) draws the box of size 400 and the boxes with size 160, but not the following ones in size, since they would be of size 160 * 0.4 = 64, which is less than 75.

Instructions:

1. Study the box function included in the boxes.cpp file. This function receives as arguments the coordinates of the upper left corner, the length of the sides and the color of the box. The function draws a box with these specifications.

2. Write a recursive algorithm for the boxes function described above. Remember to include the base case! The algorithm should also invoke the box function to draw the boxes.

3. Implement the function in QtCreator. You will need to provide additional parameters to your function so you can control the position and the color of the squares.

4. Invoke the boxes function from the main function in the main.cpp file. Compare your results with the images in Figure 6.

---

---

Deliverables

1. Use “Deliverables” in Moodle to upload the boxes.cpp and main.cpp files. Remember to use good programming techniques, include the names of the programmers involved, and to document your program.

---

---

References

[1] https://sites.google.com/a/wellesley.edu/wellesley-cs118-spring13/lectures-labs/lab-6-turtle-recursion.

[2] “Mandel zoom 00 mandelbrot set”. Licensed under Creative Commons Attribution-Share Alike 3.0 via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Mandel_zoom_00_mandelbrot_set.jpg#mediaviewer/File:Mandel_zoom_00_mandelbrot_set.jpg

[3] “Mandel zoom 04 seehorse tail”. Licensed under Creative Commons Attribution-Share Alike 3.0 via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Mandel_zoom_04_seehorse_tail.jpg#mediaviewer/File:Mandel_zoom_04_seehorse_tail.jpg

[4] http://www.coolmath.com/fractals/images/fractal5.gif

[5] “Fractal tree (Plate b - 2)”. Licensed under Public domain via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Fractaltree(Plateb-_2).jpg#mediaviewer/File:Fractaltree(Plateb-_2).jpg