repetitions-vigenerecypher/README-en.md

Repetition Structures - Vigenere Cypher

[Verano 2016 - Ive- Tatiana]

One of the advantages of using computer programs is that we can easily implement repetitive tasks. Loops such as the for, while, and do-while are control structures that allow us to repeat a block of instructions as many times as needed. These structures are also called repetition structures. In today’s lab experience, you will use for loops to complete a simple ciphering application.

Objectives:

1. Apply repetition structures to cypher a plain-text message.
2. Practice character arithmetic.

Pre-Lab:

Before coming to the lab session you should have:

1. Reviewed basic concepts related to repetition structures.

2. Reviewed basic concepts of the string class in C++, the functions length, toupper, push_back and isalpha and character arithmetic.

3. Watched Khan Academy’s “Ceasar Cypher” video at https://www.youtube.com/watch?v=sMOZf4GN3oc .

4. Watched Khan Academy’s “Vigenere Cypher” video at https://www.youtube.com/watch?v=9zASwVoshiM .

5. Studied the concepts and instructions for the laboratory session.

6. Taken the Pre-Lab quiz, available in Moodle.

---

---

Cryptography

Cryptography is the area of knowledge that studies the theory and methods that are used for protecting information so that non-authorized persons cannot understand it. A cryptographic system is a system that transforms a clear text message (a message that is understandable to humans) to a cyphered text (text that is unintelligible to unauthorized persons). Authorized persons can decypher the cyphered text to obtain the original cleartext.

The Caesar Cypher

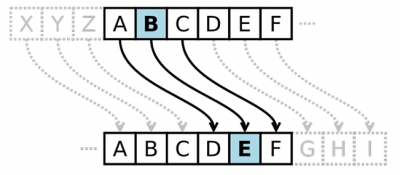
The Caesar Cypher is a substitution encryption technique that is said to have been used by Julius Caesar (100 BC - 44 BC), the Roman political and military leader, to communicate with his generals. To encrypt a message using the Caesar Cypher each letter of the clear text message is substituted by the letter found a given number of positions ahead in the alphabet. You may think of this as a shift of the letter in the alphabet. Figure 1 illustrates a shift of 3 spaces within the alphabet. For instance, letter ‘B’ would be substituted by letter ‘E’.

---

Figure 1. Caesar Cypher with shift of three.

---

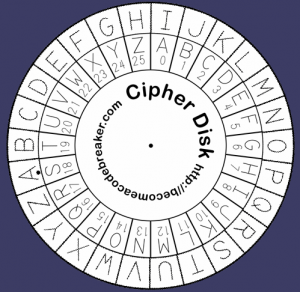
Example 1. With a shift of three, the word “ARROZ” is ciphered as “DUURC”. Observe that, with the shift of 3, letter ‘Z’ is ciphered as letter ‘C’. Any shift that takes us beyond letter ‘Z’ starts again at letter ‘A’. This is called cyclic shift. Figure 2 illustrates a circular shift of eight positions.

---

Figure 2. A Caesar cypher disk showing a shift of 8 positions.

---

Using the Modulo Operator

Modular addition is essential for implementing ciphering systems in programming. In the Caesar Cypher application above we could think that every letter of the (English) alphabet is assigned a number between 0 and 25 (‘A’ is 0, ‘B’ is 1, .., ‘Z’ is 25). The Caesar Cypher transforms every letter we convert to its corresponding number in the range [0,25], then add the displacement. To do the cyclic displacement, every time our displacement gives us a letter that corresponds to a number greater than 25, we take the remainder of the number divided by 26 and use the letter that corresponds to the remainder. Note that taking the remainder by dividing the number by 26 gives us results that will be between 0 and 25, which are the values associated with the alphabet.

The remainder of dividing two integers can be obtained using the modulo operator: %.

Going back to Example 1, in the word “ARROZ”, the letter ‘Z’ corresponds to the number 25; by having a displacement of 3 spaces, we add 3 to 25 and that results in 28 which is greater than 25. If we take the remainder of the division of $25+3$ by 26, (25+3) % 26, we obtain 2, that corresponds to the letter ‘C’.

The process above works if we can associate the letter from ‘A’ to ‘Z’ with the number from 0 to 25. This is achieved using the numeric value of the characters. As in the ASCII code, the value of the letters from ‘A’ to ‘Z’ go from 65 to 90, we need to make an adjustment in the calculation so that the A is assigned to 0. To convert an uppercase letter to a number in the range [0, 25] we only need to subtract the number 65 ('A' - 65 = 0, 'Z' - 65 = 25). To change a value from the range [0, 25] to the uppercase letter corresponding to the ASCII code, we only need to add 65 to the number. For example, the number 3 corresponds to the letter that has an ASCII code of $3 + 65 = 68$, the letter ’D’.

Figure 3 shows the pseudocode of an algorithm for the Caesar cypher. Each letter ‘c’ in the cleartext message is converted to a number in the range 0,25. The displacement d is then added to the number (modulo 26) . Lastly, the result of the modular addition is converted back to its corresponding letter by adding the ASCII code of ‘A’.

---

    Input: msg: a string of the cleartext message, d: the displacement
    Output: Caesar ciphered message 

    1. cypheredText = ""
    2. for each character c in msg:
           c = ascii(c) - ascii('A')  # map c from [‘A’,’Z’] to [0,25]
           c = ( c + d ) % 26         # circular shift c by d positions
           c = ascii(c) + ascii('A')  # map c from [0,25] to [‘A’,’Z’]
           cypheredText.append(c) 
    3. return cypheredText 

Figure 3. Pseudocode for a Caesar Cypher Algorithm.

---

The Caesar cypher is considered a weak encryption mechanism because it can easily be deciphered by using frequency analysis on the ciphered message. For example, we can use the fact that letter ‘e’ is the most frequent letter in most texts. If we find the most frequent letter in a ciphered text it probably corresponds to the letter that was substituted by ‘e’. With this information, we can compute the displacement that was used and decipher the rest of the message.

The Vigenere Cypher

The main weakness of the Caesar cypher is that every letter in the clear text message is shifted by the same number of positions. The Vigenere cypher is a somewhat stronger encryption method because the shift used on each letter is not constant. The Caesar cypher receives as an input a clear text message and a displacement, while the Vigenere receives as a data entry the clear text message and keyword that determines the displacement that will have every letter in the clear text message.

Example 2. Assume for the moment that both the message and the keyword are the same length. For example, suppose that the cleartext is “PET” and the keyword is “BED”. Each letter in the keyword determines the shift amount of the corresponding letter in the cleartext: letter ‘A’ specifies a shift of 0, ‘B’ is a shift of 1, and so on. Thus, the ‘B’ in the keyword “BED” states that we shall shift the first letter of the cleartext by 1, the ‘E’ states that we will shift second the letter by 4 and the ‘D’ states that we will shift the last letter by 3. The final result will be “QIX” as shown in Figure 4.

---

cleartext	P	E	T
keyword	B	E	D
ciphered text	Q	I	X

Figure 4. Letter ‘P’ in the cleartext is shifted by 1 to ‘Q’ as indicated by the corresponding letter in the keyword (B). Letter ‘E’ in the cleartext is shifted by 4 to ‘I’ as indicated by the corresponding letter in the keyword (E). Letter ‘T’ in the cleartext is shifted by 3 to ‘X’ as indicated by the corresponding letter in the keyword (D).

---

Figure 5 shows a table that can be used to determine the Vigenere-ciphered letter, given the clear text and keyword letter. Notice that each row contains the entire alphabet shifted by the amount specified by the letter at the beginning of the row.

---

Figure 5. Table for the Vigenere-cypher. The shaded row and column illustrate how to cypher the letter ‘R’ with key letter ‘M’.

---

If the keyword is shorter than the clear text, the Vigenere cypher simply repeats the keyword as many times as needed to account for all the letters of the clear text. Figure 6, illustrates the keyword and cleartext pairing for an example.

---

cleartext	P	R	O	G	R	A	M		T	H	I	S
keyword	S	H	O	R	T	S	H	O	R	T	S	H
ciphered text	H	Y	C	X	K	S	T		K	A	A	Z

Figure 6. Alignment of a cleartext with a shorter keyword and the resulting cypher.

---

Functions that will be used in this laboratory experience:

The program that you will be modifying in today’s experience uses the following methods of the string class:

• length: Returns the length of a string object, i.e. the number of characters in the string (including invisible characters such as the space and end-line). To invoke the length method of string object write .length() after the object’s name, e.g. msg.length().

• push_back(char c): adds the character passed as argument to the end of the string. For example, the instruction msg.push_back(‘a’) adds character a to the end of an object called msg.

We will also use the following functions:

• char toupper(char c): given a character as an argument, this function returns the character in uppercase. For example, toupper(‘b’) returns B.

• int isalpha(char c): Given a character as an argument, this function returns a non-zero value when the character is a letter. Otherwise it returns 0. As you know, C++ interprets non-zero values as true and zero as false. Thus, for example, the call isalpha(‘3’) returns false. The call returns isalpha(‘f’) returns true.

---

---

!INCLUDE “../../eip-diagnostic/vigenere/en/diag-vigenere-01.html”

!INCLUDE “../../eip-diagnostic/vigenere/en/diag-vigenere-02.html”

!INCLUDE “../../eip-diagnostic/vigenere/en/diag-vigenere-03.html”

---

---

Laboratory Session:

You will be completing an application to cypher a message using the Vigenere technique. To simplify coding, the keyword and clear text must consist exclusively of letters. Furthermore, your program must change both the cleartext and keyword to uppercase before ciphering.

Exercise 1 - Keyword and Cleartext of the Same Length

In this exercise, you will implement a function that given a cleartext and keyword of equal length returns the cypher message.

Instructions

1. Load the project VigenereCypher into QtCreator. There are two ways to do this:

   • Using the virtual machine: Double click the file VigenereCypher.pro located in the folder /home/eip/labs/repetitions-vigenerecypher of your virtual machine.
   • Downloading the project’s folder from Bitbucket: Use a terminal and write the command git clone http:/bitbucket.org/eip-uprrp/repetitions-vigenerecypher to download the folder repetitions-vigenerecypher from Bitbucket. Double click the file VigenereCypher.pro located in the folder that you downloaded to your computer.

2. You will be writing your code in the cypher.cpp file. In this file, the cypher function receives a message and a keyword of equal length and that consist exclusively of letters, and returns the Vigenere-ciphered message. Your task is to finish the implementation of the cypher function.

   Using the methods and functions discussed earlier, your implementation must verify if the message and keyword consist exclusively of letters and are of equal length. If that is not the case, the ciphered message must be (literally) "MENSAJE O CLAVE INVALIDO". Remember that your program must change both the cleartext and keyword to upper-case letters before ciphering.

3. After you implement the cypher function, go to the main function and uncomment the line that invokes test_cypher1. The test_cypher1 function is a unit test for the cypher function. It calls the cypher function with various arguments to verify if it returns correct results. If any of the results is incorrect the program stops and reports the test case that failed. You will not see the application’s graphical user interface until the unit test passes all validations. Once you see the graphical user interface you may continue onto the next part of this lab experience.

Exercise 2 - Keyword and Cleartext of Arbitrary Lengths

In this exercise, you will modify the code for the cypher function from Exercise 1 so that the application can now cypher a message using a keyword of arbitrary length.

Instructions

1. Modify the implementation of the cypher function so that it can cypher a message with a keyword of any (non-zero) length. For this exercise the message may contain any character (including non alphabetical characters). The keyword must consist exclusively of letters.

   Whenever the character in the cleartext is not a letter it will not be ciphered, as seen in Figure 7. If any character in the keyword is not a letter, the ciphered message will be (literally) ”CLAVE INVALIDA”.

   ---

   cleartext	P	R	@	G	R	*	M		T	8	I	S
   keyword	S	H	O	R	T	S	H	O	R	T	S	H
   ciphered text	H	Y	@	X	K	*	T		K	8	A	Z

   Figure 7. Example Vigenere cypher of the cleartext “PR@GR*M T8IS” using the keyword SHORT”.

   ---

2. After you implement the cypher function, modify the main function so that the line that invokes test_cypher2 is uncommented, and the line that invokes test_cyper1 is commented. Once again, you will not see the app’s graphical user interface until the test_cypher2 verifications.

---

---

Deliverables

Use “Deliverable” in Moodle to upload the cypher.cpp file that contains the cypher function that you created in Exercise 2. Remember to use good programming techniques, include the names of the programmers involved, and document your program.

---

---

References

http://www.nctm.org/uploadedImages/Classroom_Resources/Lesson_Plans/